同じ断面積をもつ梁に、同じスパンで同じ荷重を作用させた場合でも、
梁の断面を横長にした場合と、縦長にした場合で
曲がり方(中央部のたわみの大きさ)が異なります。
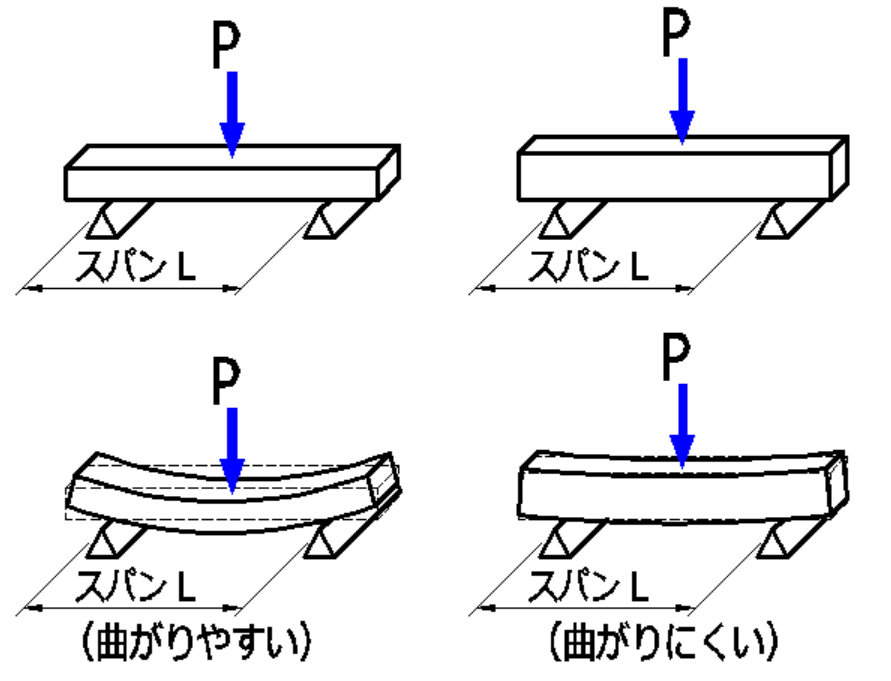
この曲がりやすい、曲がりにくいは、何の影響によるものなのか
説明していきたいと思います。
梁の曲げ剛性
曲げ剛性
梁の曲がりにくさ(=梁の曲げに対する剛性)のことを
梁の曲げ剛性といいます。
梁の曲げ剛性は、はりの材料(ex:やわらかい材料なのか硬い材料なのか)の性質と
梁の断面形状(ex:縦長なのか横長なのか)で決まります。
式で表すと
\(曲げ剛性=材料の定数(E)\times断面の定数(I)\)
となります。曲げ剛性(\(EI\))が大きいほど、曲がりにくいということになります。
【関連記事】<たわみとは>
ヤング係数
ヤング係数とは、ヤング率ともいい材料の硬さを示す材料定数で、
実験などによって求められています。
単位は(\(N/mm^2\))です。
弾性係数、もしくは、縦弾性係数とも呼ばれます。
【関連記事】<ひずみとは><フックの法則(弾性変形)>
断面一次モーメント
ある断面積\(A\)を構成する微小断面(\(dA1,dA2,・・・dAn\))に任意の座標軸(\(x軸、y軸\))からの距離をそれぞれ掛けたものを、足し合わせたものです。図で表すと下図になります。
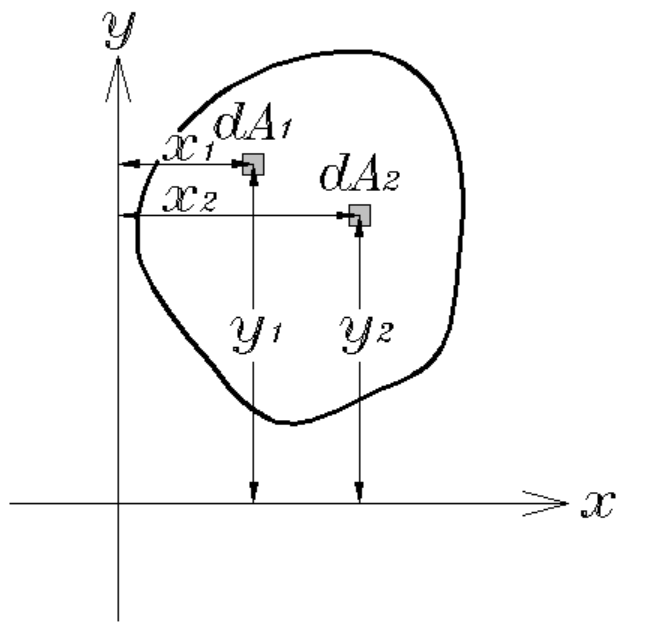
式で表すと、\(x軸\)に関する断面一次モーメントは
\(Sx=dA_1\times\)\(y\)\(_1+dA_2\times\)\(y\)\(_2+・・・dA_n\times\)\(y\)\(_n\)
\(=\sum{dA_n\times{y}_n}\)\(=\int{y}\)・\(dA\)
\(y軸\)に関する断面一次モーメントは、
\(Sy=dA_1\times\)\(x\)\(_1+dA_2\times\)\(x\)\(_2+・・・dA_n\times\)\(x\)\(_n\)
\(=\sum{dA_n\times{x}_n}\)\(=\int{x}\)・\(dA\)
となります。単位は(\(mm^3\))です。
断面一次モーメントは、断面の図心を求めるときや、
梁のせん断応力度を求めるに必要なファクターです。
図心に関する断面一次モーメントはゼロになります。
図心とは
断面一次モーメントがゼロになる点を図心といいます(禅問答みたいですね)。
断面を一点で支えられることができる点になります。
材料の密度・厚みが均一の場合は、図心が重心になります。
<例題>
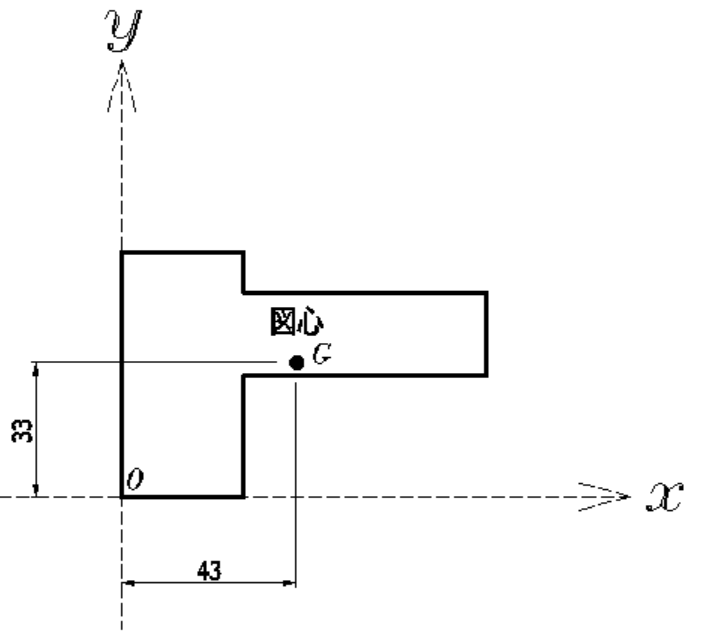
下図の図心を求めてみたいと思います。
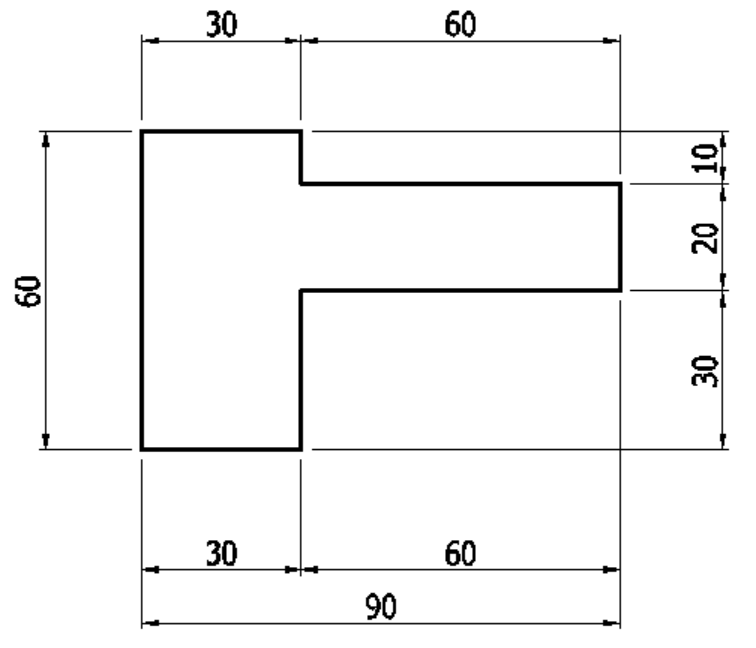
CADソフトを使うとワンクリックで求めることができます。
それを言ったら元も子もないので、電卓を使って求めていきましょう。
まず、縦長の長方形を\(A1\)、横長の長方形を\(A2\)として
それぞれ\(0点\)からの断面一次モーメントを算出します。
長方形の図心は、対角線の交点なので、
簡単にそれぞれの図心までの距離は出せますね。
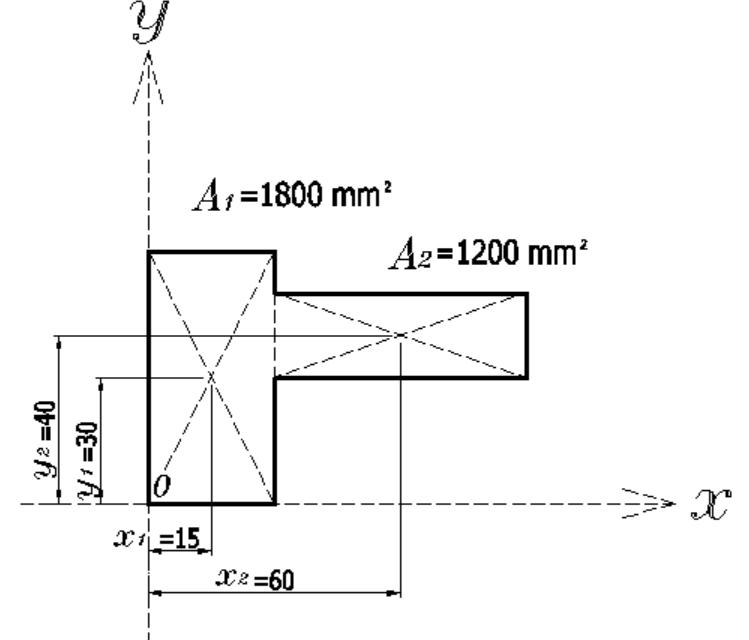
\(Sx_1=x_1\times\)\(A_1=15\times1800=27000mm^3\)
\(Sx_2=x_2\times\)\(A_2=60\times1200=72000mm^3\)
\(Sx_0=Sx_1+Sx_2=27000+72000=99000mm^3\)・・・(1)
\(Sy_1=y_1\times\)\(A_1=30\times1800=81000mm^3\)
\(Sy_2=y_2\times\)\(A_2=40\times1200=48000mm^3\)
\(Sy_0=Sy_1+Sy_2=81000+48000=129000mm^3\)・・・(2)
\(A_0=A_1+A_2=1800+1200=3000mm^2\)・・・(3)
図心の座標を(\(x_0,y_0\))とすると、(1)(2)(3)より
\(x_0=\Large{\frac{Sx_0}{A_0}}\)\(=\Large{\frac{99000}{3000}}\)\(=33mm\)
\(y_0=\Large{\frac{Sy_0}{A_0}}\)\(=\Large{\frac{129000}{3000}}\)\(=43mm\)
下図のようになります。
最初の方で断面一次モーメントは「足し合わせたもの」と定義しているので
断面一次モーメント同士は、足したり引いたりできます。
断面二次モーメント

断面二次モーメントは、ある断面Aを構成する微小断面(\(dA_1,dA_2,\cdots{,dA_n}\))に
任意の座標軸(\(x\)軸・\(y\)軸)からの距離の2乗を
それぞれ掛けたものを、足し合わせたものです。
式で表すと、\(x軸\)に関する断面二次モーメントは
\(I_x=dA_1\times{y_1^2}+dA_2\times{y_2^2+}\cdots{+dA_n}\times{y_n^2}\)
\(=\sum{dA_n}\times{y_n^2}=\int{y^2}\cdot{dA}\)
同様に、\(y軸\)に関する断面二次モーメントは
\(I_y=dA_1\times{x_1^2}+dA_2\times{x_2^2}+\cdots{+dA_n}\times{x_n^2}\)
\(=\sum{dA_n}\times{x_n^2}=\int{x^2}\cdot{dA}\)
となります。単位は(\(mm^4\))です。

図心外の任意の軸に関する断面二次モーメントは、
\([図心外の軸に関する断面二次モーメント]\)
\(=[図心軸に関する断面二次モーメント]+[面積]\times[(図心軸までの距離)^2]\)
で求めることができます。
\(I_x=I_{nx}+A\times{y_0^2}\)
\(I_y=I_{ny}+A\times{x_0^2}\)
上式から
1)図心軸に関する断面二次モーメントはゼロになりません。
2)図心軸に関する断面二次モーメントは、
これと平行な他の軸に対する断面二次モーメントより、
常に小さくなります(=図心軸の断面二次モーメントが最も小さい値になる)。
ということがわかります。
図心軸に関しての値がゼロにならないというと、
距離を2乗しているので、マイナス座標の値もプラスになり、
足し合わせたときに打ち消されなくなるためです。
断面二次モーメントは、部材の曲げに対する強さや
たわみを求めるときに必要なファクターです。
断面係数
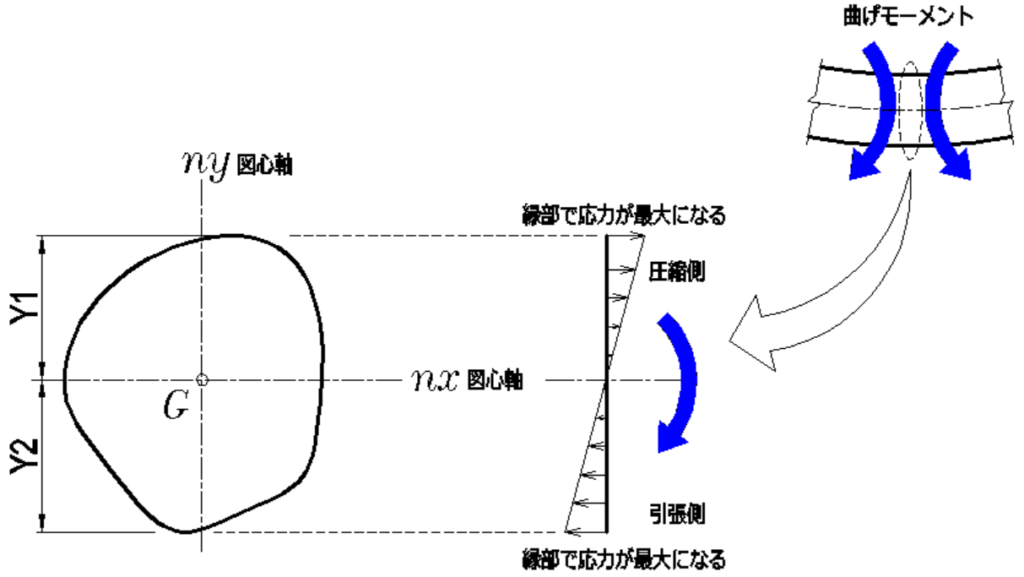
断面の図心軸に関する断面二次モーメントを、
軸から断面の両縁までの距離で割った値を断面係数といいます。
断面係数は、曲げ応力度が最大となる縁応力度(ふちおうりょくど)
を求める際の係数として使われます。
単位は(\(mm^3\))です。
式で表すと、
\([断面係数]\)\(=\Large{\frac{[図心軸に関する断面二次モーメント]}{[図心を通る軸から断面の端までの距離]}}\)
\(Z_1=\Large{\frac{I_{nx}}{Y_1}}\)
\(Z_2=\Large{\frac{I_{nx}}{Y_2}}\)
断面係数は、断面一次モーメント、断面二次モーメントのときのように
分割して求めて、あとで足し合わせることができません。
断面係数というものが、断面全体の図心軸に関する断面二次モーメントを求めてから、
縁までの距離で割って求めるものだからです。
【関連記事】<縁応力度とは>
断面二次半径
断面二次半径は、座屈の計算をするときに用いられる定数です。単位は(\(mm\))です。
図心を通る軸からの距離を\(i\)として、
この位置での全断面\(A\)の二次モーメント(\(i^2\times{A}\))が
断面二次モーメント\(I\)と等しくなるとき、
この図心を通る軸からの距離\(i\)を断面二次半径といいます。
\(I_x=i_x^2\times{A}\)
\(I_y=i_y^2\times{A}\)
より、断面二次半径は
\(i_x=\sqrt{\Large{\frac{I_x}{A}}}\)
\(i_y=\sqrt{\Large{\frac{I_y}{A}}}\)
と表されます。
これは、図心を通る軸の断面二次モーメントを断面積で割って平方根に入れたものです。
弱軸に関する断面二次半径が、座屈の計算では重要になってきます。
座屈は、弱軸方向に起こるためです。
弱軸=断面二次モーメントが最も小さくなる図心軸のことです。
【関連記事】<強軸・弱軸とは(主軸とは)>
まとめ
断面の性質が決まるファクター
\(E\):ヤング係数(=ヤング率)(\(N/mm^2\))
⇒材料の硬さを表します。
\(S\):断面一次モーメント(\(mm^3\))
⇒図心を求めるのに使用します。
\(I\):断面二次モーメント(\(mm^4\))
⇒断面形状の曲げ強さを表します。
\(Z\):断面係数(\(mm^3\))
⇒縁応力度を求めるときに使用する係数です。
\(A\):断面二次半径(\(mm\))
⇒座屈の計算をするときに使用します。
ヤング係数と断面二次モーメントを掛けたもの(=E×I)を曲げ剛性と呼ばれます。

