梁に荷重Pが作用したとき、
梁が赤色線のように変形した場合の変形量(変位量)をたわみといいます。
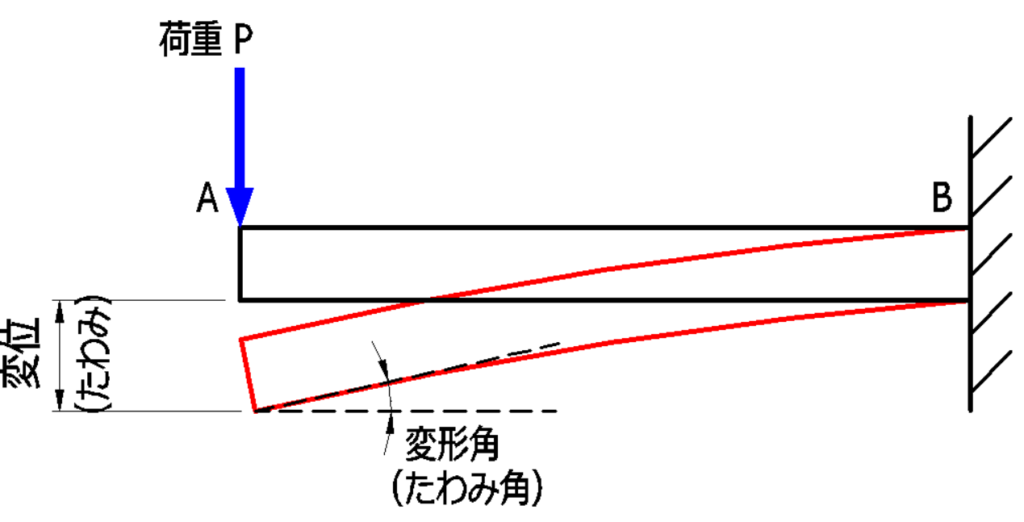
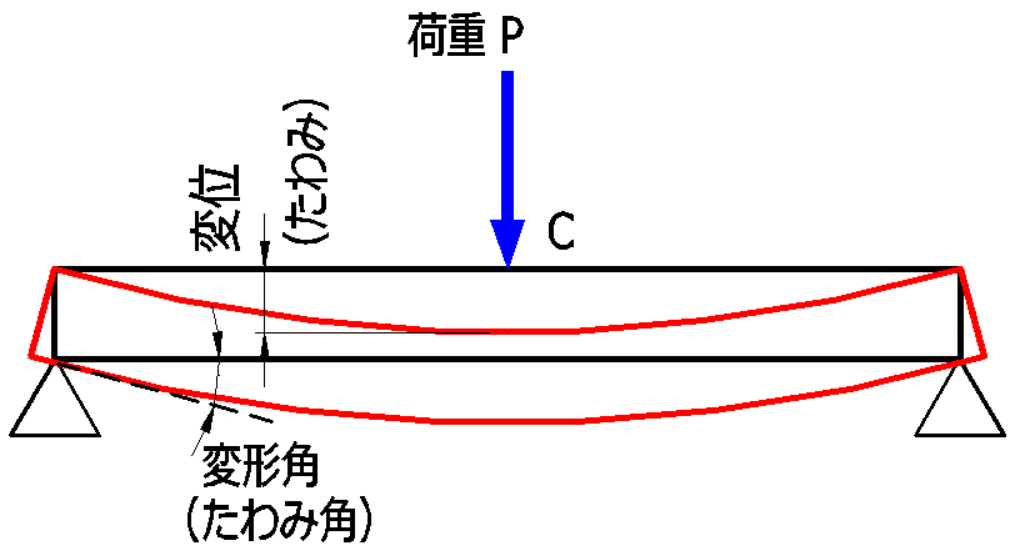
たわみは、梁の曲げ剛性 E・I に左右されます(反比例します)。
E:ヤング係数(梁の材料の特性)
I:断面二次モーメント(梁の断面の特性)
【関連記事】<ヤング係数とは・断面二次モーメントとは>
たわみ量(δ)とは
たわみ量は、たわみの変位量のことで、長さで表されます。
単に、「たわみ」といわれたら、たわみ量の事を指します。
たわみ角(θ)とは
たわみが生じている角度のことを、たわみ角といいます。
通常、単位はラジアンで表されます。
たわみ量・たわみ角の公式
たわみ量・たわみ角を求める式は、仮想仕事の原理などから求めます。
ここでは、公式を丸暗記して欲しいパターンのものを紹介します。
片持ち梁のたわみ
先端に集中荷重が作用するパターン
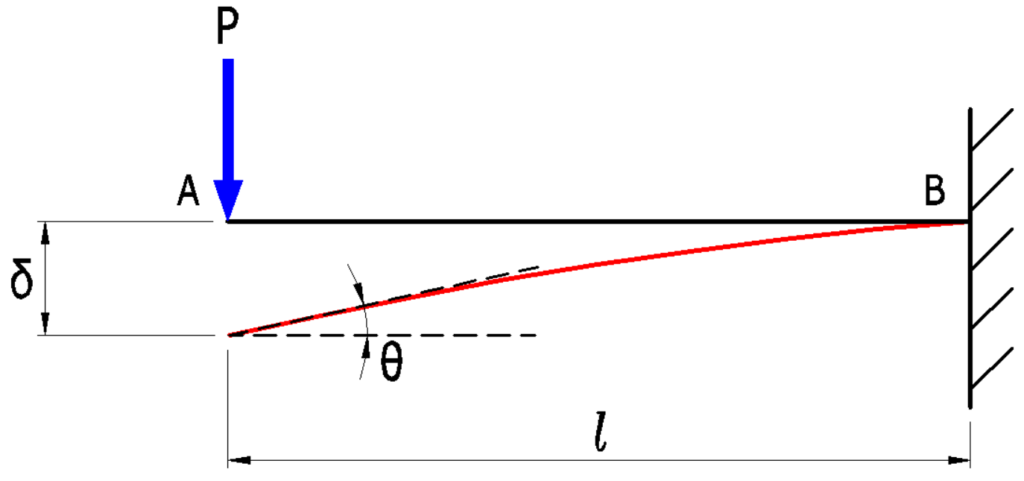
\(\delta_A=\Large{\frac{Pl^3}{3EI}}\)(\(mm\))
\(\theta_A=\Large{\frac{Pl^2}{2EI}}\)(\(rad\))
等分布荷重が作用するパターン
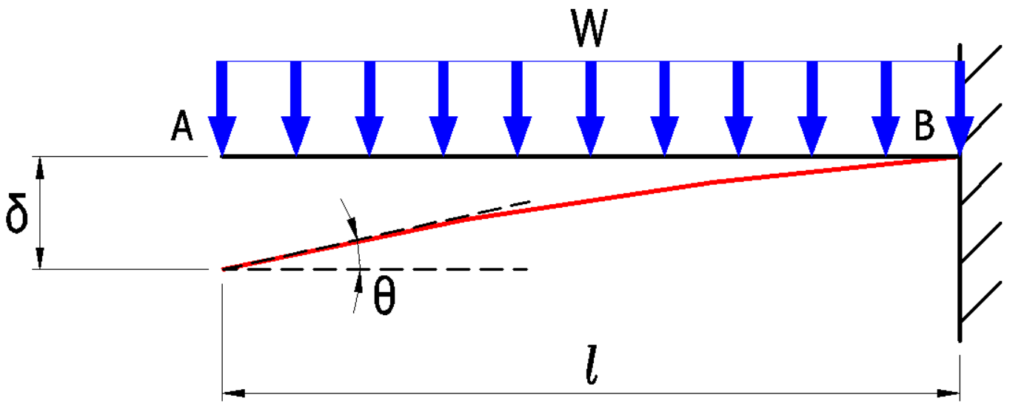
\(\delta_A=\Large{\frac{wl^4}{8EI}}\)(\(mm\))
\(\theta_A=\Large{\frac{wl^3}{6EI}}\)(\(rad\))
先端にモーメントが作用するパターン
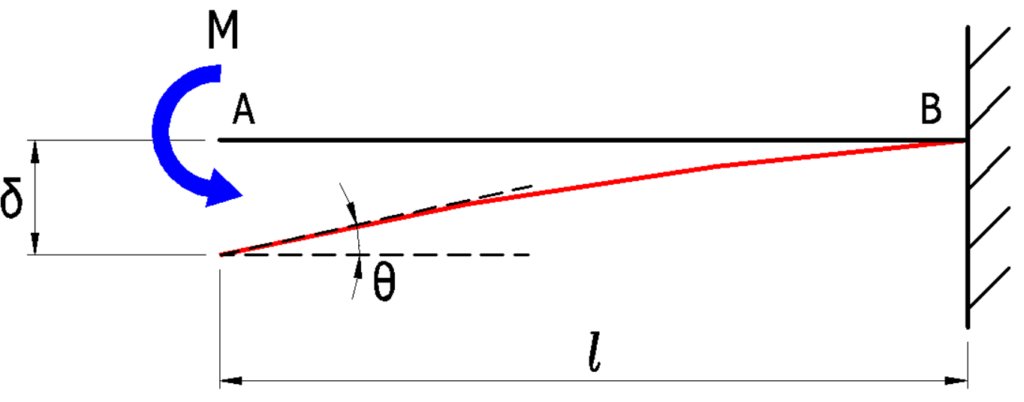
\(\delta_A=\Large{\frac{Ml^2}{2EI}}\)(\(mm\))
\(\theta_A=\Large{\frac{Ml}{EI}}\)(\(rad\))
単純梁のたわみ
中央に集中荷重が作用するパターン
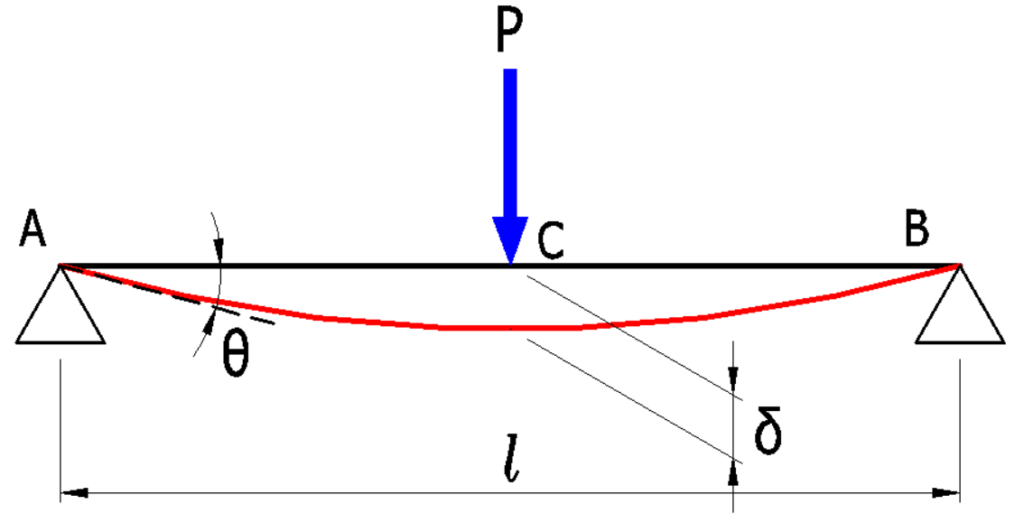
\(\delta_C=\Large{\frac{Pl^3}{48EI}}\)(\(mm\))
\(\theta_A=\Large{\frac{Pl^2}{16EI}}\)(\(rad\))
全体にわたり等分布荷重が作用するパターン
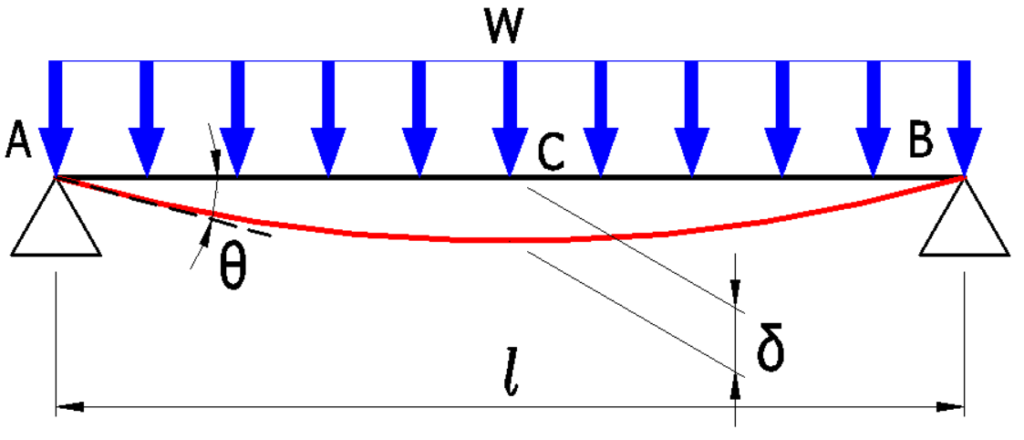
\(\delta_C=\Large{\frac{5wl^4}{384EI}}\)(\(mm\))
\(\theta_A=\Large{\frac{wl^3}{24EI}}\)(\(rad\))
まとめ
梁に荷重が作用したときの変形量をたわみといいます。
たわみ量は梁の曲げ剛性・支持条件・作用する荷重の条件で変化します。

