応力とひずみ
部材に外力が作用すると、部材の内部には、これに抵抗する力が発生します。
この部材内部で生じている力の流れを応力といいます。
また、応力の発生と同時に、部材にも何等かの変形を生じます。
この部材の変形をひずみといいます。
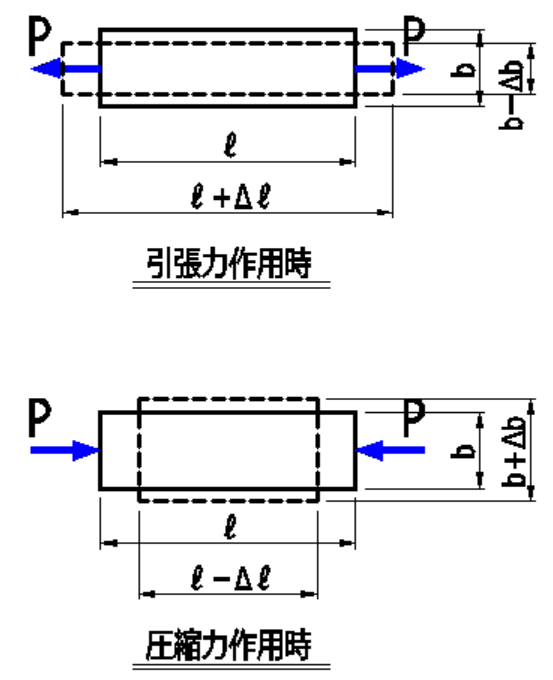
長さ\(l\)の材料に、軸方向力が作用したとき、
これによる軸方向のひずみ量(引張力の場合は伸び、圧縮力の場合は縮み)を\(Δl\)とすると、
単位長さ当たりのひずみを、垂直ひずみ度(\(\varepsilon_l\))といいます。
\(\varepsilon_l=\Large{\frac{Δl}{l}}\)(無名数)
で表されます。
また、同時に生じる軸と垂直方向のひずみ量(引張力の場合は縮み、圧縮力の場合は伸び)を\(Δb\)
もとの長さを\(b\)とすると、軸と垂直方向の単位長さ当たりのひずみを
横ひずみ度(\(\varepsilon_b\))といいます。
\(\varepsilon_b=\Large{\frac{Δb}{b}}\)(無名数)
ひずみ量=長さの単位があります
ひずみ(ひずみ度)=割合なので無名数
ポアソン比とは
ポアソン比(\(\nu\))は、垂直ひずみ度に対する横ひずみ度の割合です。
\(ポアソン比\nu=\Large{\frac{横ひずみ度}{垂直ひずみ度}}\)=\(\Large{\frac{\varepsilon_b}{\varepsilon_l}}\)
で表されます。
材料が受ける応力が弾性限度以内の場合、
垂直ひずみ度(\(\varepsilon_l\))と横ひずみ度(\(\varepsilon_b\))の比は
材料によって一定であることを
フランス人のポアソン氏が発見しました。この定数\(m\)をポアソン数といいます。
\(m=\Large{\frac{\varepsilon_l}{\varepsilon_b}}\)\(=\Large{\frac{Δl}{l}}\)\(\div\Large{\frac{Δb}{b}}\)\(=\Large{\frac{Δl}{Δb}}\)\(\times\Large{\frac{b}{l}}\)\(=一定\)
ポアソン比は、このポアソン数の逆数です。
\(\nu=\large{\frac{1}{m}}\)
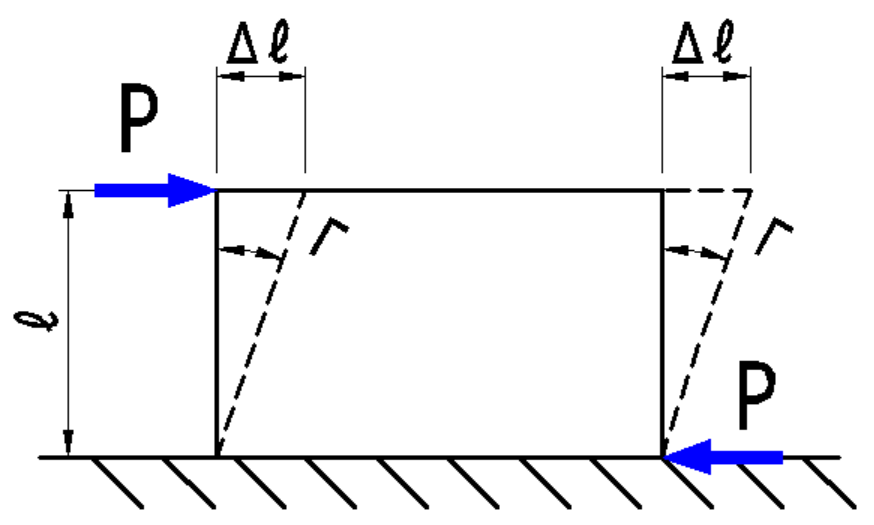
せん断ひずみとは
下図のように、平行四辺形のようにずれる変形をせん断ひずみ(\(\gamma\))といいます。
\(\gamma=\Large{\frac{Δl}{l}}\)(無名数)
応力度とは
部材に生じている応力の大小を比較するため
単位面積当たり(\(mm^2\))の応力(\(N\))であらわします。
応力度の単位は(\(N/mm^2\))です。
(材料力学では、\(MPa\)を使用する参考書もあります)
\(1N/mm^2=1MPa\)
\(M(メガ)=10^6\)
\(1Pa=1N/m^2\)
単位の変換
応力度には、
- 曲げ応力度 :曲げモーメントにより生じる応力度
- せん断応力度 :せん断力により生じる応力度
- 引張応力度 :軸方向力により生じる応力度(+)
- 圧縮応力度 :軸方向力により生じる応力度(-)
があります。
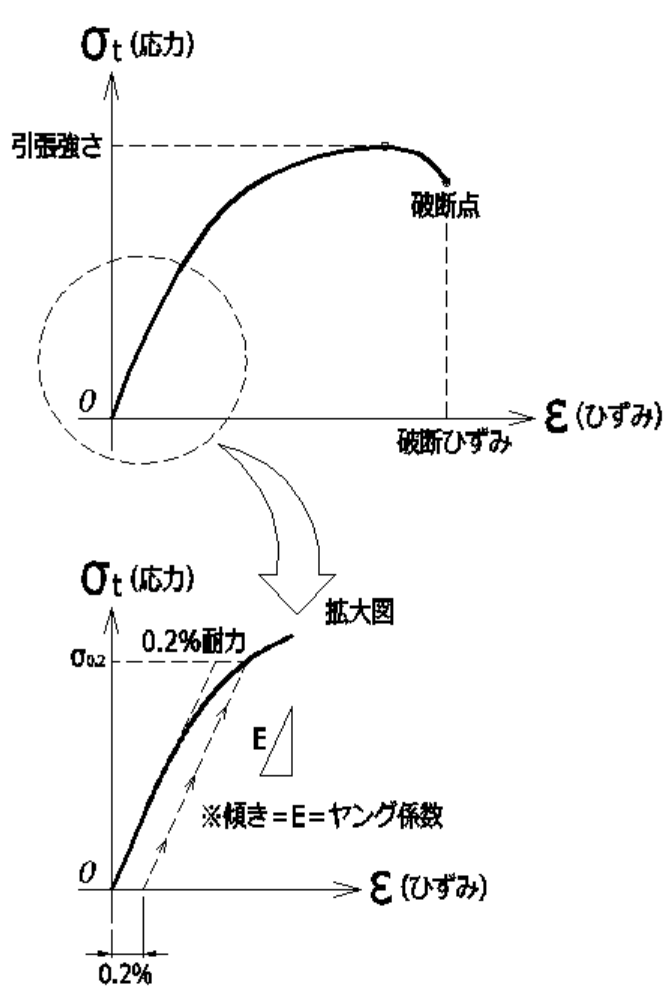
応力・ひずみ曲線とは
材料に軸方向力(引張力もしくは圧縮力)を加え
そのときの応力度とそれに対応するひずみ度の関係をグラフに表したものです。
下図は、鋼材の引張試験の場合の応力・ひずみ曲線の概形です。
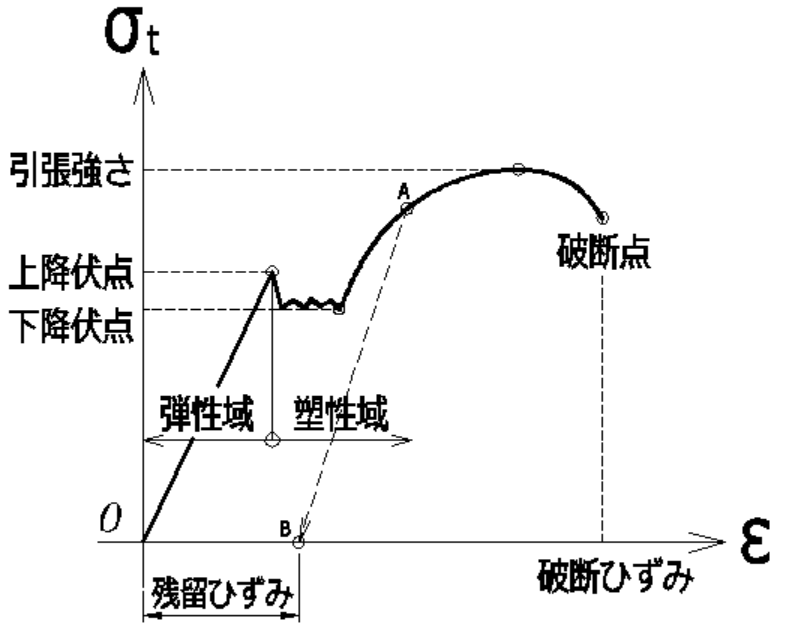
フックの法則(=弾性変形(弾性域))
弾性変形(=弾性域)とは、応力の増加とひずみの増加が比例関係の状態です。
この比例関係時の比例定数にあたる定数が、ヤング係数(ヤング率)(\(E\))です。
ヤング係数は、縦弾性係数と呼ばれることもあります。
\(\sigma=E\times{\varepsilon}\)
\(E=\Large{\frac{\sigma}{\varepsilon}}\)\(=\Large{\frac{\frac{P}{A}}{\frac{Δl}{l}}}\)\(=\Large{\frac{P\times{l}}{A\timesΔl}}\)(\(N/mm^2\))
ヤング係数は、材料ごとに一定の値をもっています。
この応力とひずみの比例関係のことをフックの法則といいます。
弾性範囲内では、荷重をゼロに戻すと、変形もゼロに戻ります。
降伏点とは
弾性変形の限界の応力を降伏応力といいます。
鋼材では、上図のように上降伏点と下降伏点が示されますが
応力値は下降伏点の値が限界値としてを用いられます。
(ex:SS400材の場合\(=235N/mm^2\))
つまり、SS400材の場合、応力度が\(235N/mm^2\)を超えると
荷重をゼロに戻しても変形が残ってしまう、ということです。
塑性変形(=塑性域)とは
上図応力・ひずみ曲線のAまで荷重をかけ、荷重をゼロに戻すと、
ひずみはBだけ残ります。これを残留ひずみといいます。
強い力をかけて曲げたら、曲がりっぱなしの状態のまま、ということです。
金属の加工では、この塑性変形を利用しています。
塑性域で変形を続けていくと、金属の結晶結合にダメージが蓄積されていきます。
このダメージがある一定レベルを超えるとくびれを生じてその後、破断します。
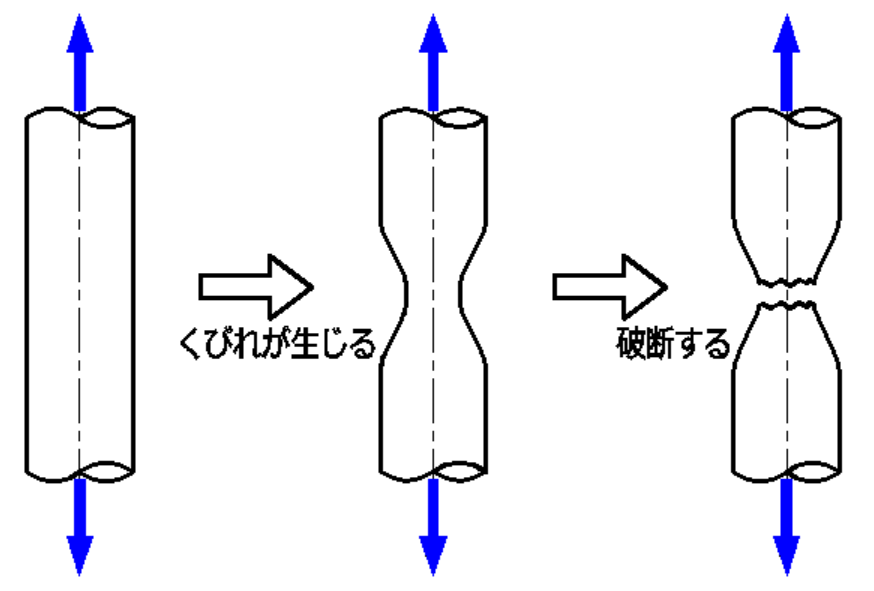
くびれは、部材の最も弱い部分に生じます。
このくびれが生じる直前に、応力は最大値になります(=引張強さ)。
また、破断時のひずみを破断ひずみといいます。
ミルシート(鋼材の材料の品質を保証する保証書)には、
降伏点・引張強さ・破断ひずみが記載されています。
0.2%耐力とは
SS400材のように、応力・ひずみ曲線で明確な降伏点がわかる材料もありますが、
アルミニウムやステンレスのように、明確な降伏点を示さずに塑性変形が始まる材料もあります。
ひずみが0.2%のときの応力度を降伏応力のめやすにしておこう。
と決めたのが、0.2%耐力です。
降伏点がわからないと、弾性域と塑性域の区別がつけられないので、
不便なことが多いためです。
まとめ
部材に外力が作用すると、部材内部に応力が生じます。
この応力により生じる変形をひずみ(ひずみ度)といいます。
ポアソン比は、垂直ひずみ度に対するよこひずみ度の割合です。
応力度は、単位面積当たりに作用する応力を表します。
応力度は、材料の評価によく使用します。
応力・ひずみ曲線とは、応力に対するひずみをグラフで表したものです。
弾性域とは、フックの法則が成立する範囲のことです。
塑性域とは、変形が元に戻らない領域のことです。

