曲げ応力とは
曲げモーメントによって梁の内部に生じる応力を曲げ応力といいます。
曲げ応力は引張と圧縮の偶力による回転力により生じます。
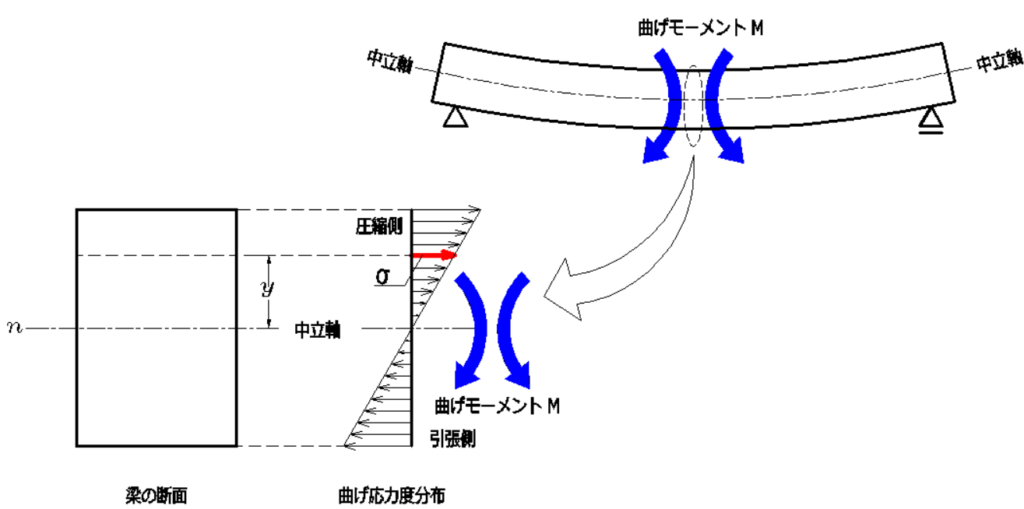
\(\sigma\):曲げ応力度(\(N/mm^2\))(プラスは引張、マイナスは圧縮)
\(M\):外力による曲げモーメント(\(N\cdot{mm}\))
\(I_n\):中立軸に関する断面二次モーメント(\(mm^4\))
\(y\):\(\sigma\)を求めようとする位置の中立軸からの距離(\(mm\))
\(\sigma=\pm\Large{\frac{M}{I_n}}\)\(・y\) (\(N/mm^2\))
縁応力度とは
「ふちおうりょくど」と読みます。
断面の上縁・下縁で起きる曲げ応力度の最大値です。
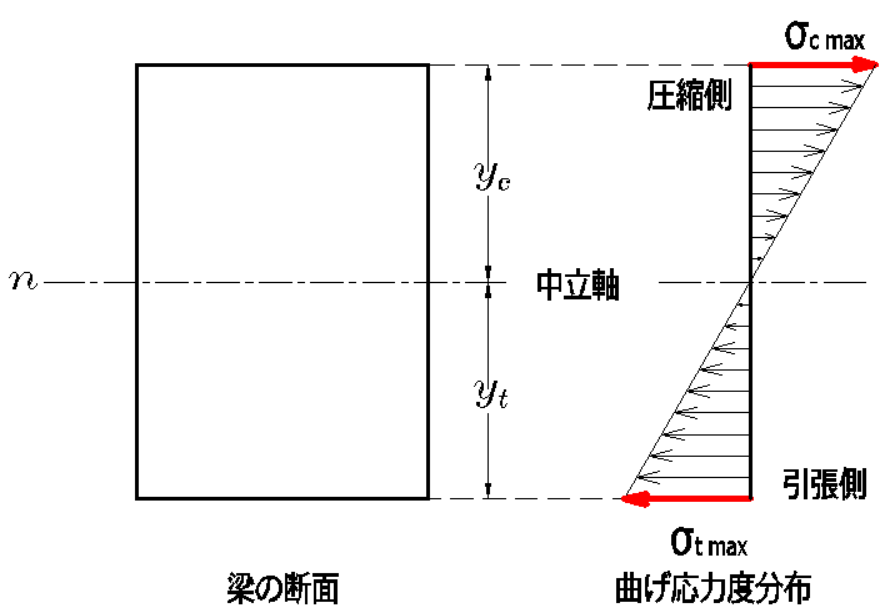
\(\sigma_{c-max},\sigma_{t-max}\)を縁応力度といいます。
\(Z_c\):上縁の断面係数
\(Z_t\):下縁の断面係数
\(Z_c=\Large{\frac{I_n}{y_c}}\)
\(Z_t=\Large{\frac{I_n}{y_t}}\)
とすると、縁応力度は、
\(\sigma_{c-max}=\Large{\frac{M}{I_n}}\)\(・y_c=\Large{\frac{M}{Z_c}}\)(\(N/mm^2\))
\(\sigma_{t-max}=\Large{\frac{M}{I_n}}\)\(・y_t=\Large{\frac{M}{Z_t}}\)(\(N/mm^2\))
となります。
通常、梁の曲げ応力度を検証する場合は
この縁応力度を曲げ応力度の値として用います。
【関連記事】<断面係数とは>
中立面(中立軸)とは
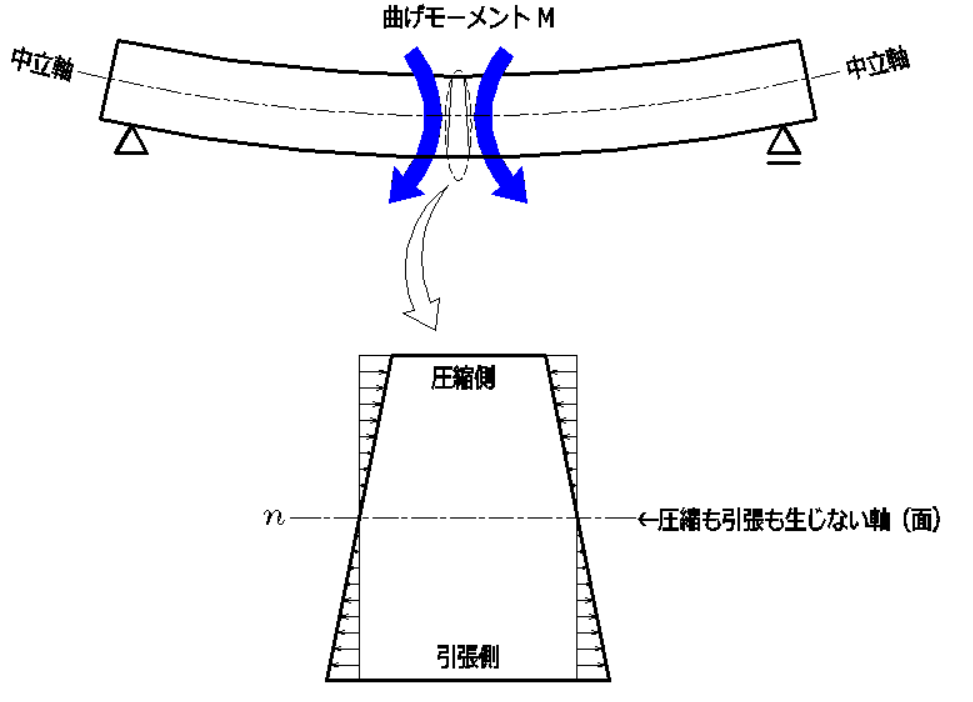
梁の内部に曲げ応力度が生じたときに、圧縮も引張も生じない面
(=伸びも縮みも生じない面)があります。
これを中立軸といいます。
曲げ応力度(縁応力度)の導き出し方
仮定条件
・変形はフックの法則が成り立つ範囲内とする(\(\sigma=E\cdot\varepsilon\))
・梁の横断面は、変形後も平面である
・梁の変形は、曲げモーメントのみによって生じるものとする
曲げモーメントによる梁の変形(1)は、(2)のように描き変えることができます。
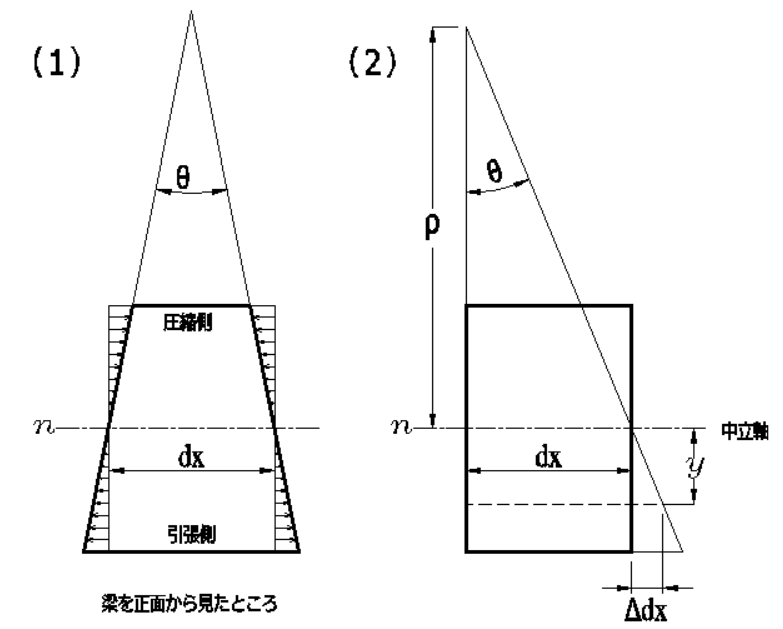
\(Δdx\):中立軸から\(y\)の位置のひずみ(\(mm\))とすると
\(\varepsilon=\Large{\frac{Δdx}{dx}}\)\(=\Large{\frac{y}{\rho}}\)
\(\sigma_x=E\cdot{\varepsilon}=E\cdot\Large{\frac{y}{\rho}}\)
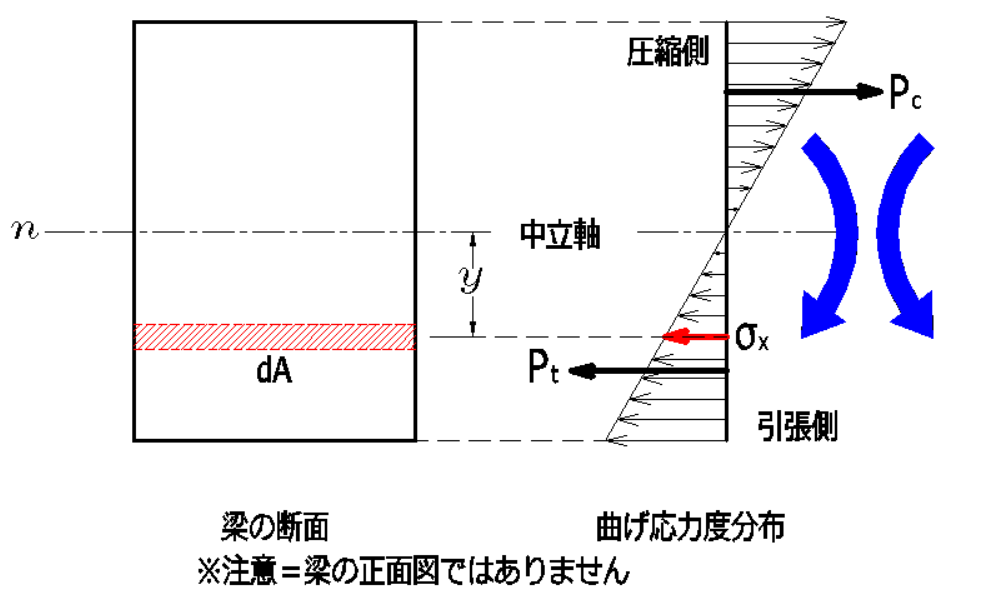
応力のつりあいを考えます。
\(\Sigma{H}=0\)より
\(\Sigma{H}=\int{\sigma_x\cdot{dx}}=\int{E}\Large{\frac{y}{\rho}}\)\(dx\)
\(=\Large{\frac{E}{\rho}}\)\(\int{y\cdot}dA=0\)
\(\int{y\cdot}dA=0\)
上式は、断面一次モーメントをあらわしており、
断面一次モーメントがゼロであるから、中立軸は図心軸と等しいことを示しています。
続いて、引張応力度の合力を\(P_t\)、圧縮応力度の合力を\(P_c\)とすると、
\(P_t=P_c\)
の偶力であることがわかります。
次に、
\(\Sigma{M}=0\)より
この偶力のモーメントと外力のモーメント(\(=M\))が等しいことになります。
偶力のモーメント\(=\int(\sigma_x\cdot{dA})y\)
\(M=\int(\sigma_x\cdot{dA})y\)
\(=\int(E\Large{\frac{y}{\rho}}\)\(dA)y\)
\(=\Large{\frac{E}{\rho}}\)\(\int{y^2}\cdot{dA}\)
上式の「\(\int{y^2}\cdot{dA}\)」は、中立軸に関する断面二次モーメントであるので、これを\(I_n\)とする、また
\(\sigma_x=E\cdot\Large{\frac{y}{\rho}}\)から
\(\Large{\frac{E}{\rho}}\)\(=\Large{\frac{\sigma_x}{y}}\) となるので、
\(M=\Large{\frac{E}{\rho}}\)\(\cdot{I_n}\)
\(M=\Large{\frac{\sigma_x}{y}}\)\(\cdot{I_n}\)
\(\sigma_x=\Large{\frac{M}{I_n}}\)\(\cdot{y}\)
縁応力度は、\(y=y_c(=圧縮側の最大値),y_t(=引張側の最大値)\)のときの値であるので、
\(\sigma_{c-max}=\Large{\frac{M}{I_n}}\)\(\cdot{y_c}\)\(=\Large{\frac{M}{Z_c}}\)
\(\sigma_{t-max}=\Large{\frac{M}{I_n}}\)\(\cdot{y_t}\)\(=\Large{\frac{M}{Z_t}}\)
\(Z_c=\Large{\frac{I_n}{y_c}}\):圧縮側の断面係数(\(mm^3\))
\(Z_t=\Large{\frac{I_n}{y_t}}\):引張側の断面係数(\(mm^3\))
【関連記事】<断面二次モーメント・断面係数とは>

