強軸・弱軸とは
断面が曲げ荷重に対して、
最も抵抗が大きい(=曲げづらい)かつ図心を通る軸を強軸といいます。
強軸の断面二次モーメントは最大になります。
強軸に直交する軸が弱軸になります。
弱軸の断面二次モーメントは最小になります。
【関連記事】<断面二次モーメントとは>
弱軸は曲げ荷重に対して、最も抵抗が小さい軸ということです。
また座屈現象は、弱軸の方向に生じる特性があります。
【関連記事】<座屈とは>
主軸とは
強軸と弱軸を一対の座標系としてみたとき
この座標系を主軸といいます
(=強軸+弱軸の組み合わせを主軸と呼んでいます)
主軸は断面相乗モーメントがゼロになります。
種々断面の断面の主軸(強軸と弱軸)
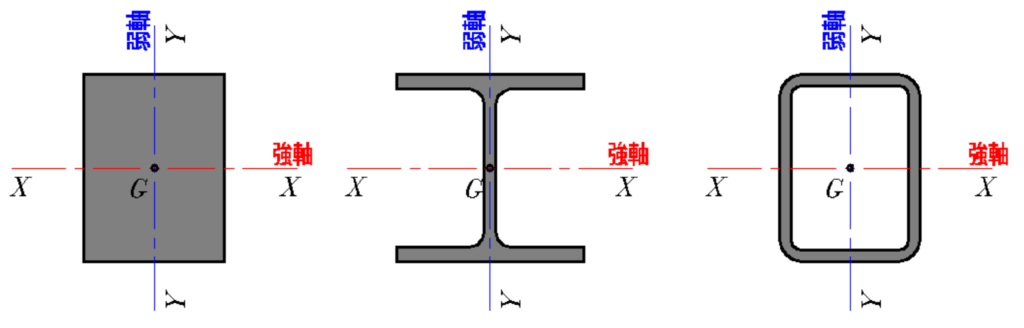
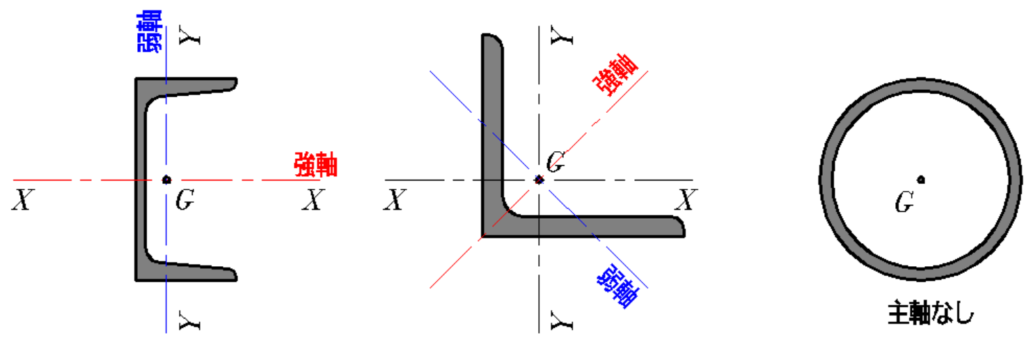
強軸に曲げ荷重がかかるように設計する断面は
経済的な断面(=断面を有効に効かせている)であるといえます。
断面相乗モーメントとは
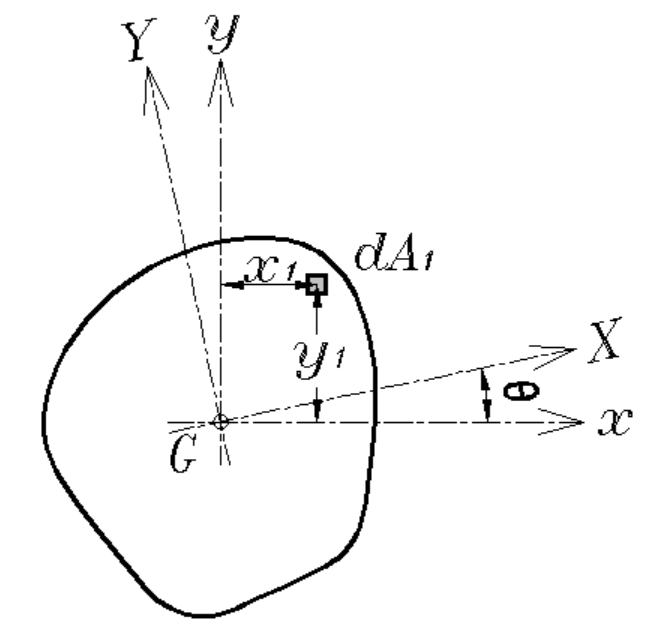
ある断面Aを構成する微小断面(\(dA_1,dA_2・・・dA_n\))に
図心を通る直交座標軸(\(x\)軸\(,y\)軸)からの距離(\(x_1\)および\(y_1\))をかけて
足し合わせたものを、断面相乗モーメント\(I_{xy}\)といいます。
\(I_{xy}=dA_1\times{x_1}\times{y_1}+dA_2\times{x_2}\times{y_2}+・・・+dA_n\times{x_n}\times{y_n}\)
\(=\sum{dA_n}\times{x_n}\times{y_n}=\int_A{xy}・dA\)(\(mm^4\))
座標軸の角度\(\theta\)を変化させていったとき、
断面相乗モーメントがゼロになる一対の座標軸が主軸になります。
種々の断面の断面二次モーメント・断面係数・断面二次半径
よくある断面の断面積・断面二次モーメント・断面係数・断面二次半径を
算出するための公式を紹介します。
長方形断面
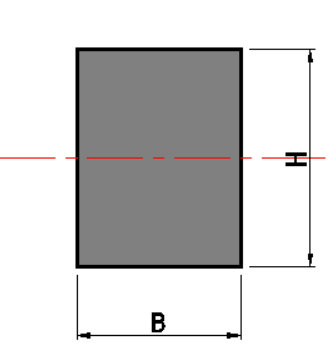
断面積 \(A=BH\)(\(mm^2\))
断面二次モーメント \(I=\Large{\frac{BH^3}{12}}\)(\(mm^4\))
断面係数 \(Z=\Large{\frac{BH^2}{6}}\)(\(mm^3\))
断面二次半径 \(i=\Large{\frac{H}{\sqrt{12}}}\)(\(mm\))
円形断面
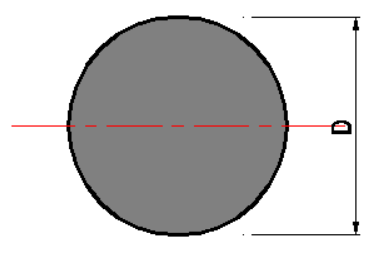
断面積 \(A=\Large{\frac{\pi{D^2}}{4}}\)(\(mm^2\))
断面二次モーメント \(I=\Large{\frac{\pi{D^4}}{64}}\)(\(mm^4\))
断面係数 \(Z=\Large{\frac{\pi{D^3}}{32}}\)(\(mm^3\))
断面二次半径 \(i=\Large{\frac{D}{4}}\)(\(mm\))
ボックス型断面
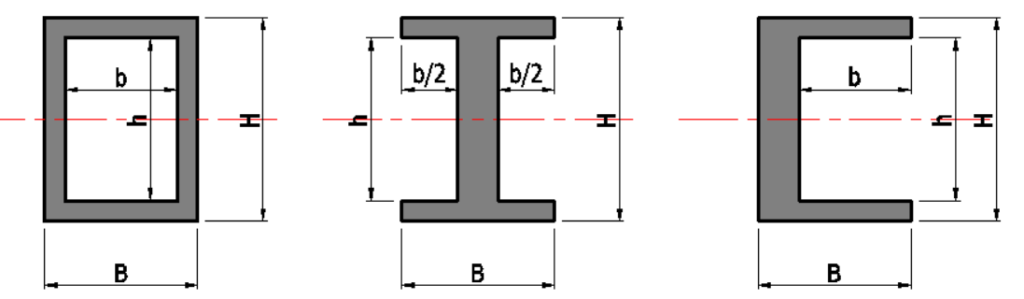
上記3形状は同じ式になります。
断面積 \(A=BH-bh\)(\(mm^2\))
断面二次モーメント \(I=\Large{\frac{BH^3-bh^3}{12}}\)(\(mm^4\))
断面係数 \(Z=\Large{\frac{BH^3-bh^3}{6H}}\)(\(mm^3\))
断面二次半径 \(i=\Large{\sqrt{\frac{BH^3-bh^3}{12(BH-bh)}}}\)(\(mm\))
H型断面
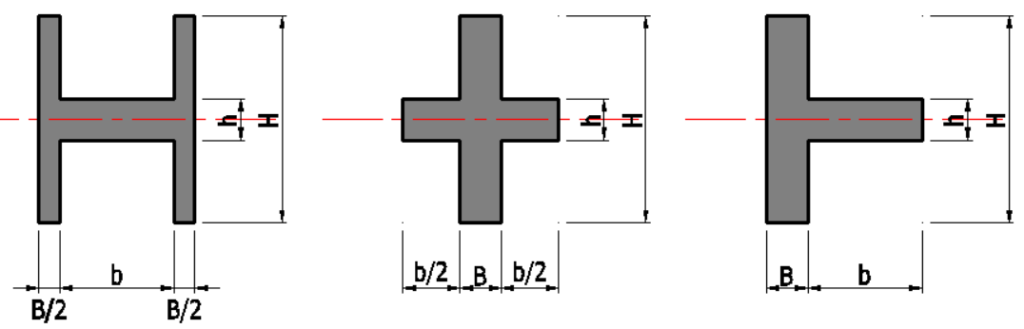
上記3形状は同じ式になります。
断面積 \(A=BH+bh\)(\(mm^2\))
断面二次モーメント \(I=\Large{\frac{BH^3+bh^3}{12}}\)(\(mm^4\))
断面係数 \(Z=\Large{\frac{BH^3+bh^3}{6H}}\)(\(mm^3\))
断面二次半径 \(i=\Large{\sqrt{\frac{BH^3+bh^3}{12(BH+bh)}}}\)(\(mm\))
ドーナツ型断面
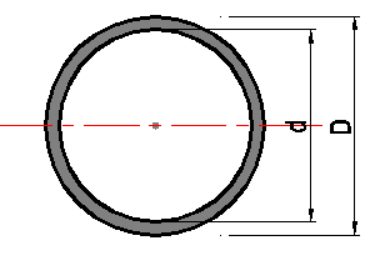
断面積 \(A=\Large{\frac{\pi}{4}}\)\((D^2-d^2)\)(\(mm^2\))
断面二次モーメント \(I=\Large{\frac{\pi}{64}}\)\((D^4-d^4)\)(\(mm^4\))
断面係数 \(Z=\Large{\frac{\pi}{32}}\)・\(\Large{\frac{D^4-d^4}{D}}\)(\(mm^3\))
断面二次半径 \(i=\Large{\frac{\sqrt{D^4+d^4}}{4}}\)(\(mm\))
三角形断面
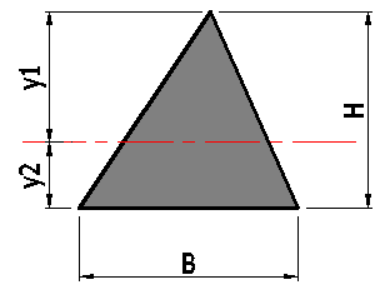
断面積 \(A=\Large{\frac{BH}{2}}\)(\(mm^2\))
断面二次モーメント \(I=\Large{\frac{BH^3}{36}}\)(\(mm^4\))
断面係数 \(Z_1=\Large{\frac{BH^2}{24}}\)(\(mm^3\)) (\(y_{1}=\Large{\frac{2H}{3}}\))
\(Z_2=\Large{\frac{BH^2}{12}}\)(\(mm^3\)) (\(y_{2}=\Large{\frac{H}{3}}\))
断面二次半径 \(i=\Large{\frac{H}{\sqrt{18}}}\)(\(mm\))
まとめ
強軸とは、曲げ荷重に対して最も抵抗が大きくなる図心を通る断面軸です。
(=断面二次モーメントが最大になる軸)
弱軸とは、強軸と直交する軸で、曲げに対して最も抵抗が小さくなる軸です。
(=断面二次モーメントが最小になる軸)
強軸と弱軸をあわせた一対の座標軸を主軸といいます。
主軸の断面相乗モーメントはゼロになります。
断面性能の公式を暗記するのは、長方形断面くらいで大丈夫だと思います。
\(\Large{\frac{断面二次モーメント}{縁までの距離}}\)\(=断面係数\)
\(\sqrt{\Large{\frac{断面二次モーメント}{断面積}}}\)\(=断面二次半径\)
など、それぞれの関係を覚えておくと役に立つと思います。

