ヤング係数比とは
コンクリートに対する鉄筋のヤング係数の比のことをヤング係数比といいます。
断面を設計し、その性質(断面一次モーメント・断面二次モーメントなど)を評価するときに
単一材料な断面で計算・検討する方が便宜上都合がいいためこの係数比を用います。ヤング係数比は、
\(n=\Large{\frac{E_s}{E_c}}\)
で求められます。
\(E_s\):鉄筋のヤング係数⇒\(2.05\times10^5\)(\(N/mm^2\))
\(E_c\):コンクリートのヤング係数(下式より算出)
\(\gamma\):コンクリートの単位体積重量(\(kN/m^3\))
\(F_c\):コンクリートの設計基準強度(\(N/mm^2\))
\(E_c=3.35\times10^4\times(\Large{\frac{\gamma}{24}}\)\()^2\times(\Large{\frac{F_c}{60}}\)\()^{\frac{1}{3}}\)(\(N/mm^2\))・・・(1-1)
断面設計用ヤング係数比
鉄筋コンクリート構造計算規準・同解説(2010年)では、
コンクリートに対する鉄筋のヤング係数比を下表のように定めています。
| コンクリートの設計基準強度 \(F_c\)(\(N/mm^2\)) | ヤング係数比 n |
|---|---|
| \(F_c\leq27\) | \(15\) |
| \(27<F_c\leq36\) | \(13\) |
| \(36<F_c\leq48\) | \(11\) |
| \(48<F_c\leq60\) | \(9\) |
【関連記事】<ヤング係数>
(1-1)式に単位体積重量\(\gamma\)と設計基準強度\(F_c\)を代入して得られた数値と、
上表の数値を比べると上表の数値の方が大きな値になっています。
弾性計算値より大きい値なのはなぜか
コンクリートは、クリープ現象の影響を受けるので、
クリープの影響を考慮する必要があるからです。
【関連記事】<クリープとは>
(1-1)式は、コンクリートの弾性的性質をもとに実験から求めた式です。
=クリープの影響を受ける前のコンクリートのヤング係数になります。
クリープが生じると、コンクリートの見かけ上のヤング係数は小さくなります。
=見かけ上、コンクリートがやわらかくなるということです。
=結果として、鉄筋の応力負担が大きくなります。つまり、ヤング係数比は大きくなります。
⇒クリープの影響を考慮するならば、ヤング係数比は相対的に大きくなります。
仮に、クリープの影響を考慮したヤング係数比で、断面を設計するとどうなるでしょうか。
ヤング係数比が(相対的に)大きいので、
=圧縮側の鉄筋の断面積が小さくなります。=圧縮側のコンクリートの負担が大きくなります。
=コンクリートのクリープがより進行します。⇒危険側の設計になっていまします。
設計をする際には、弾性計算値のヤング係数比で設計する方が安全なのです。
しかし、現実の現象としてクリープは生じます。
最終的に落としどころとして、弾性計算値のヤング係数比と、
弾性計算値のヤング係数比を2倍したもの(=クリープを考慮した見かけのヤング係数比)
の平均を、設計用のヤング係数比として設定されたのが、上表です。
等価断面積とは
鉄筋とコンクリート、異なる材料で構成されている断面を
単一の材料であらわしたものです。
鉄筋をn倍して、コンクリートに置き換えて表現します。
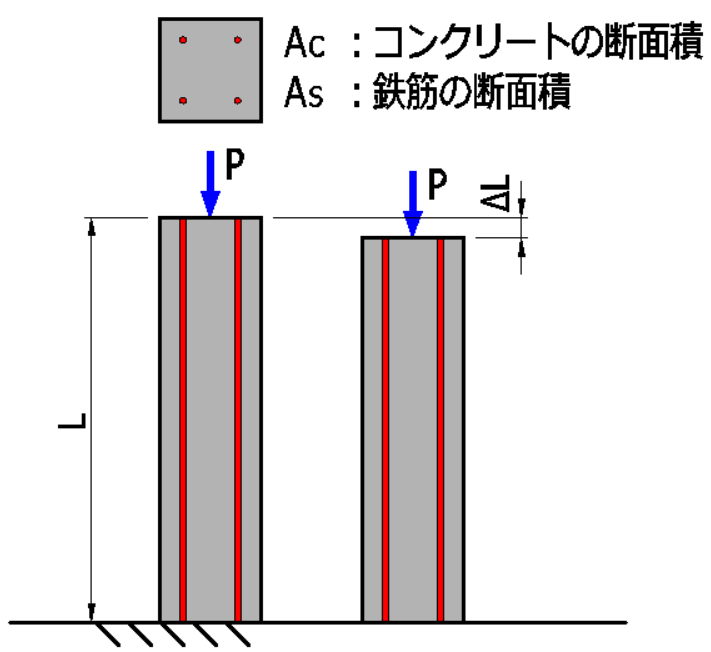
\(A_c\):コンクリートの断面積(\(mm^2\))
\(A_s\):鉄筋の断面積(\(mm^2\))
\(\sigma_c\):コンクリートの応力度(\(N/mm^2\))
\(\sigma_s\):鉄筋の応力度(\(N/mm^2\))
\(\varepsilon\):ひずみ度
ひとまず、圧縮荷重Pを表現すると、
\(P=A_c\cdot\sigma_c+A_s\cdot\sigma_s\)(\(N\))
フックの法則より
\(\sigma_c=E_c\cdot\varepsilon\)(\(N/mm^2\))
\(\sigma_s=E_s\cdot\varepsilon\)(\(N/mm^2\))
【関連記事】<フックの法則>
\(P=A_c\cdot{E_c}\cdot\varepsilon+A_s\cdot{E_s}\cdot\varepsilon\)(\(N\))
\(n\):コンクリートに対する鉄筋のヤング係数比
とおくと、
\(n=\Large{\frac{E_s}{E_c}}\) より \(E_s=n\cdot{E_c}\)
\(P=\varepsilon\cdot{E_c}(A_c+n\cdot{A_s})\)
\(=\sigma_c(A_c+n\cdot{A_s})\)(\(N\))
\(\sigma_c=\Large{\frac{P}{A_c+n\cdot{A_s}}}\)(\(N/mm^2\))
\(\sigma_s=E_s\cdot\varepsilon=n\cdot{E_c}\cdot\varepsilon=n\cdot\sigma_c\)
\(=n\cdot\Large{\frac{P}{A_c+n\cdot{A_s}}}\)(\(N/mm^2\))
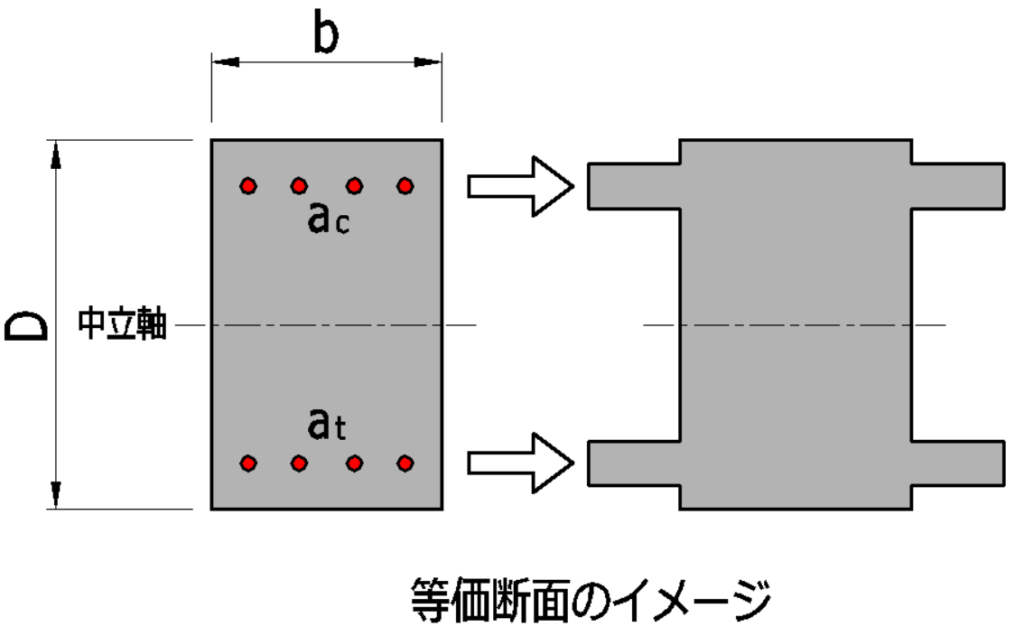
ここで\(A_e\)を等価断面積といいます。
\(A_e=A_c+n\cdot{A_s}\)(\(mm^2\))
まとめ
ヤング係数比とは、コンクリートと鉄筋のヤング係数の比のことです。
断面設計用のヤング係数比は、クリープ考慮した値(=ほぼ弾性計算値の1.5倍)
の数値に設定されています。
等価断面積とは、鉄筋コンクリートの鉄筋部分をコンクリートに置換した断面のことです。
参考文献
- 日本建築学会(2010年)「鉄筋コンクリート構造計算規準・同解説」
- 佐藤立美・荒木秀夫・森村毅(2011年)「RC規準による鉄筋コンクリートの構造設計[改訂版]」鹿島出版会

