応力とは
部材に外力が作用したとき、部材の中に生じる力を応力(断面力)といいます。
応力には、曲げモーメント・せん断力・軸方向力の3種類があります。
この3種類の力が、梁にどのように作用しているかをM図(曲げモーメント図)
・Q図(せん断力図)・N図(軸方向力図)で表します。
求めた応力(曲げモーメント・せん断力・軸方向力)は、部材の断面寸法を設計するときに利用されます。
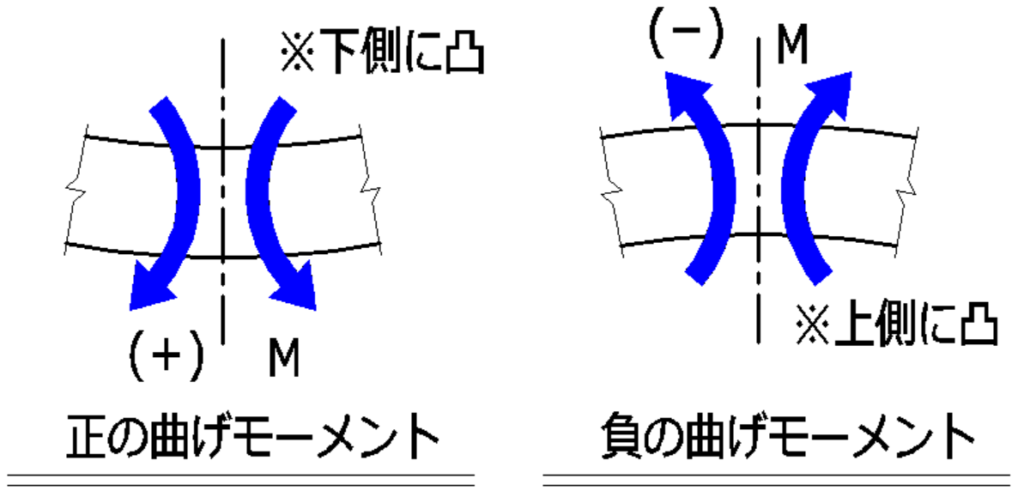
曲げモーメントとは
梁の断面をねじ込もうとする力を曲げモーメントといいます
下側に凸な曲げモーメント=正の(+)曲げモーメント
上側に凸な曲げモーメント=負の(-)曲げモーメントといいます。
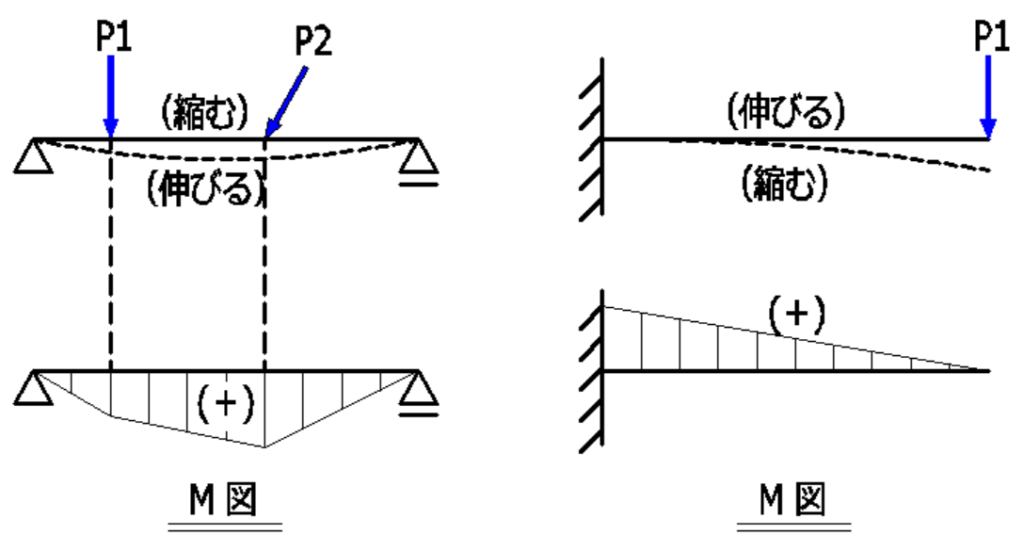
曲げモーメント図(M図)
正の曲げモーメントは基線の下に、負の曲げモーメントは基線の上に描きます。
(=梁が伸びる側(引張側)に描きます)
「曲げモーメント」
:外力によって部材を曲げようとするモーメントのことです。
「モーメント」
:任意の点を回転させようとする回転力のことです。
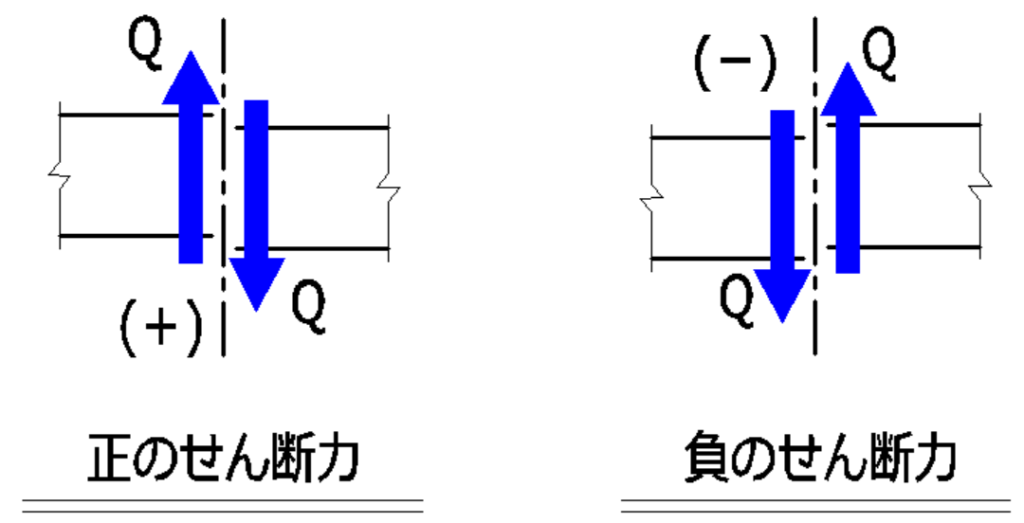
せん断力とは
梁の断面をすり切ろうとする力をせん断力といいます。
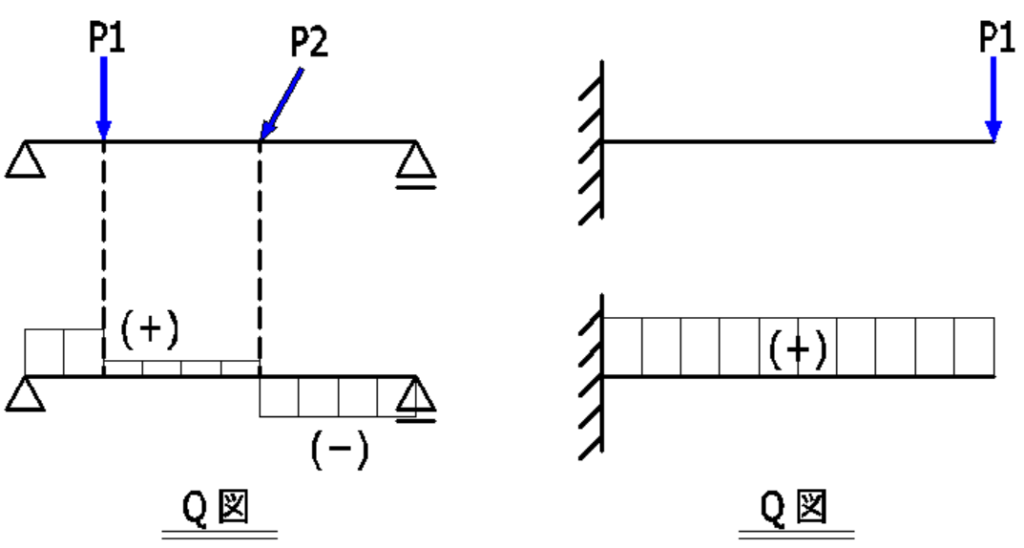
せん断力図(Q図)
正のせん断力を基線の上に、負のせん断力を基線の下に描きます。
軸方向力とは
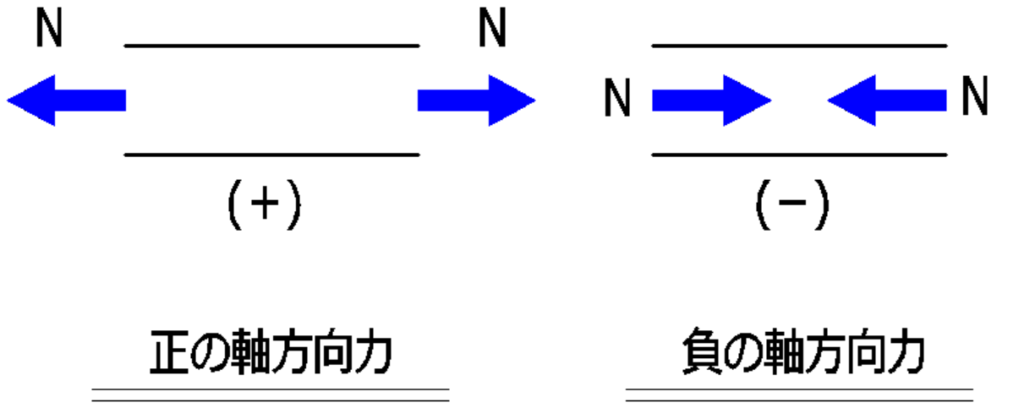
軸方向に作用する力を軸方向力(軸力)といいます。
引張力を正(+)、圧縮力を負(-)で表します。
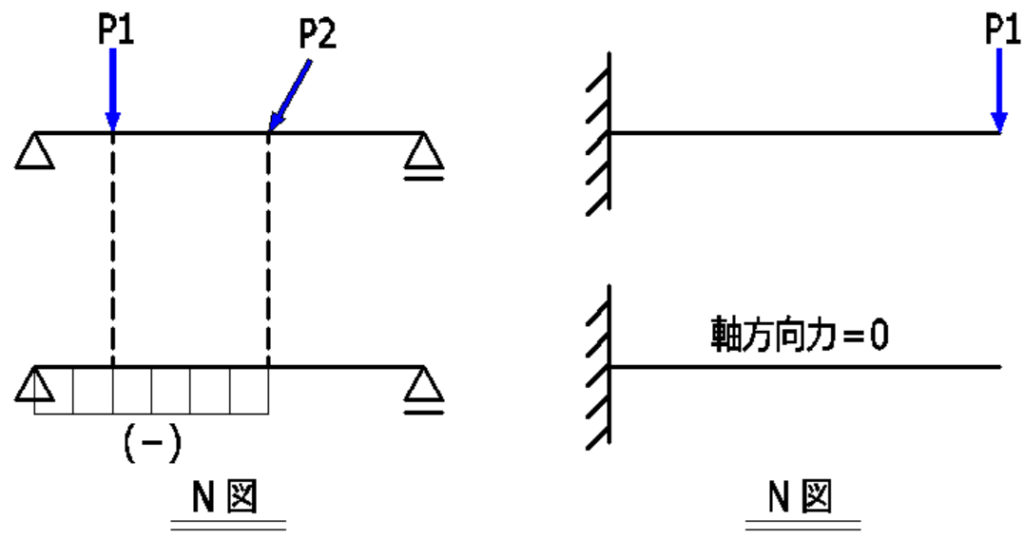
軸方向力図(N図)
正の軸方向力(=引張力)を基線の上に、負の軸方向力(圧縮力)を基線の下に描きます。
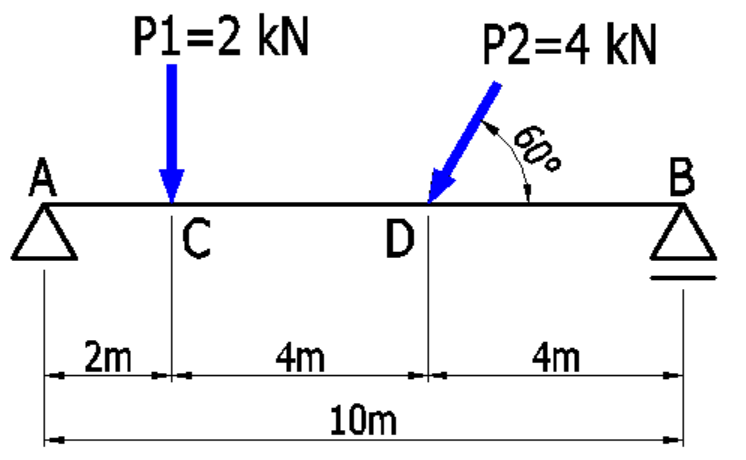
単純梁に集中荷重が作用した場合の応力図
<例題>下記に示す単純梁の応力図を具体的に求めていきます。
まず、ファーストステップは反力を求めます。
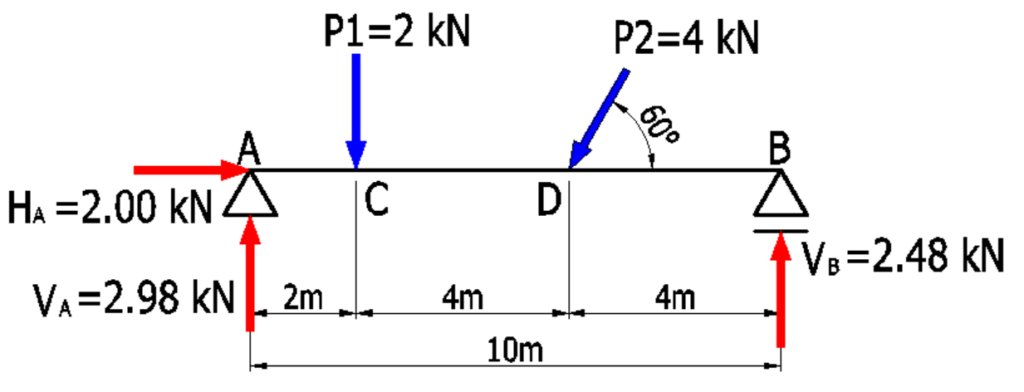
【関連記事】<単純梁の反力の算出>
このサイトでだいぶ使いまわされていますね。
熟練度があがっていくことを皆さん経験的にご存じのはずです。
例えば、野球の素振りなどは、まさにそれですね。
まず、M図から求めていきましょう。\(x\)をA→B間で動く変数として
A→C間、C→D間、D→B間のそれぞれの区間で、
梁に作用する曲げモーメントを出していきます。
(1)A→C間(\(0\le x\le2\))
\(M=2.98\times{x}\) より
\(M_A=2.98\times{0}=0\)
\(M_C=2.98\times{2}=5.96kN\cdot{m}\)
(2)C→D間(\(2\le x\le6\))
\(M=2.98\times{x}-2\times(x-2)\) より
\(M_D=2.98\times{6}-2\times(6-2)=9.88kN\cdot{m}\)
(3)D→B間(\(6\le x\le10\))
\(M=2.98\times{x}-2\times(x-2)-3.46\times(x-6)\) より
\(M_B=2.98\times{10}-2\times(10-2)-3.46\times(10-6)=0.04kN\cdot{m}\)
(※ゼロとみなします。∵三角関数を小数に丸めた際に生じた誤差のため)
(1)(2)(3)より単純梁のM図は下記のようになります。
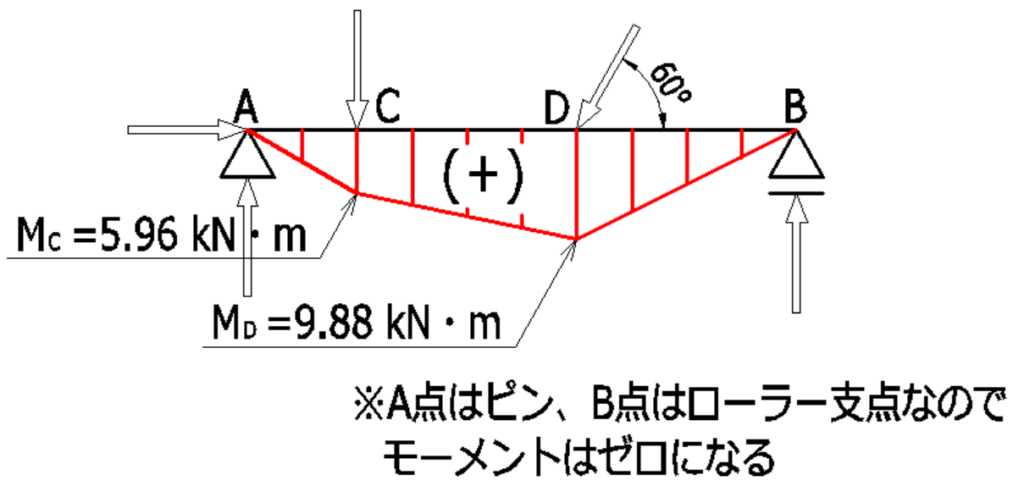
続いて、Q図を描きます。作用荷重・反力の値を落とし込んでいきながら、各点のせん断力を求めていきます。
(1)A点のせん断力
\(Q_A=V_A=2.98kN\)
(2)C点のせん断力
\(Q_C=Q_A-V_C=2.98-2.00=0.98kN\)
(3)D点のせん断力
\(Q_D=Q_D-V_D=0.98-3.36=-2.48kN\)
以上より、単純梁のQ図は下記のようになります。
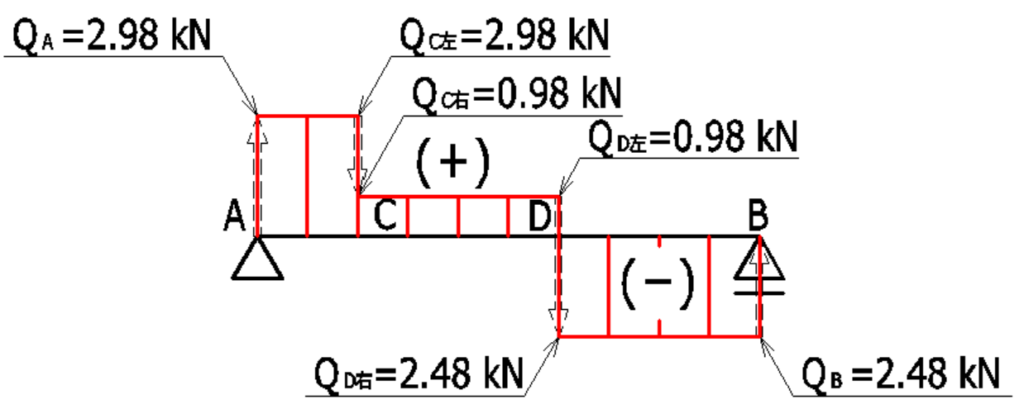
最後にN図を描きます。
N図は、引張(プラス)か圧縮(マイナス)かが非常に重要なので、注意しましょう。
(1)A→C間
\(N_A=2.00kN\)(圧縮)
(2)C→D間
\(N_C=2.00kN\)(圧縮)
(3)D→B間
\(N_B=0\)
以上より、単純梁のN図は下記のようになります。
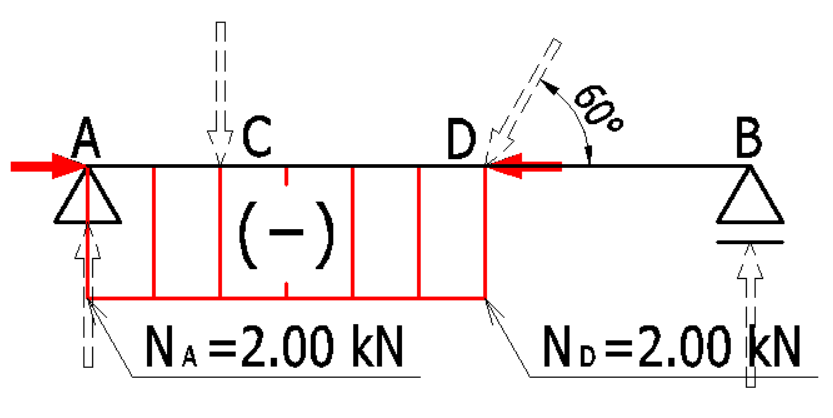
片持ち梁に集中荷重が作用したときの応力図
<例題>下記に示す片持ち梁の応力図を具体的に求めていきます。
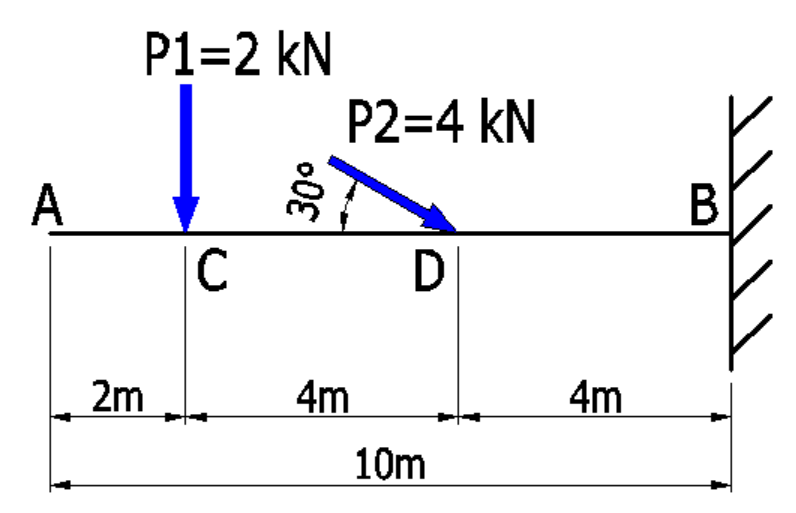
まず、ファーストステップは単純梁のときと同様で、反力を求めます。

単純梁と同様に、M図から求めていきましょう。\(x\)をA→B間で動く変数として
A→C間、C→D間、D→B間のそれぞれの区間で、
梁に作用する曲げモーメントを出していきます。
(1)A→C間(\(0\le x\le2\))
\(M=0\times{x}\) より
\(M_A=0\times{0}=0\)
\(M_C=0\times{2}=0\)
(2)C→D間(\(2\le x\le6\))
\(M=0\times{x}-2\times(x-2)\) より
\(M_D=0\times{6}-2\times(6-2)=-8.00kN\cdot{m}\)
(3)D→B間(\(6\le x\le10\))
\(M=0\times{x}-2\times(x-2)-2\times(x-6)\) より
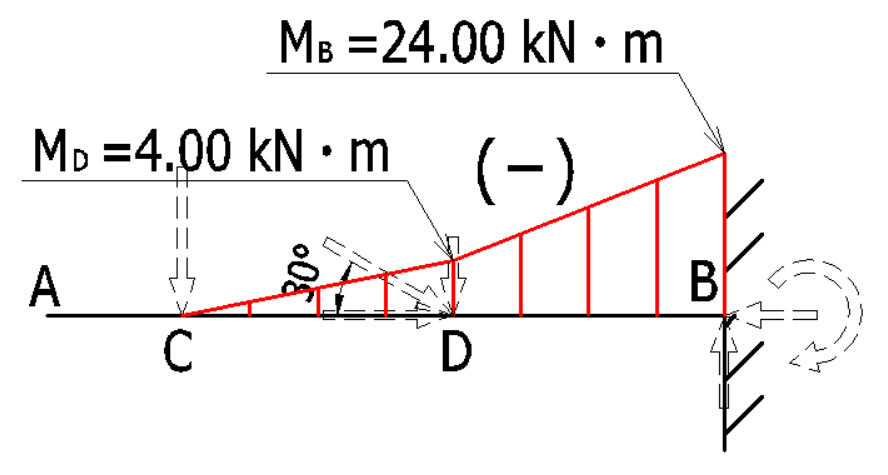
\(M_B=0\times{10}-2\times(10-2)-2\times(10-6)=-24.00kN\cdot{m}\)
(1)(2)(3)より片持ち梁のM図は下記のようになります。
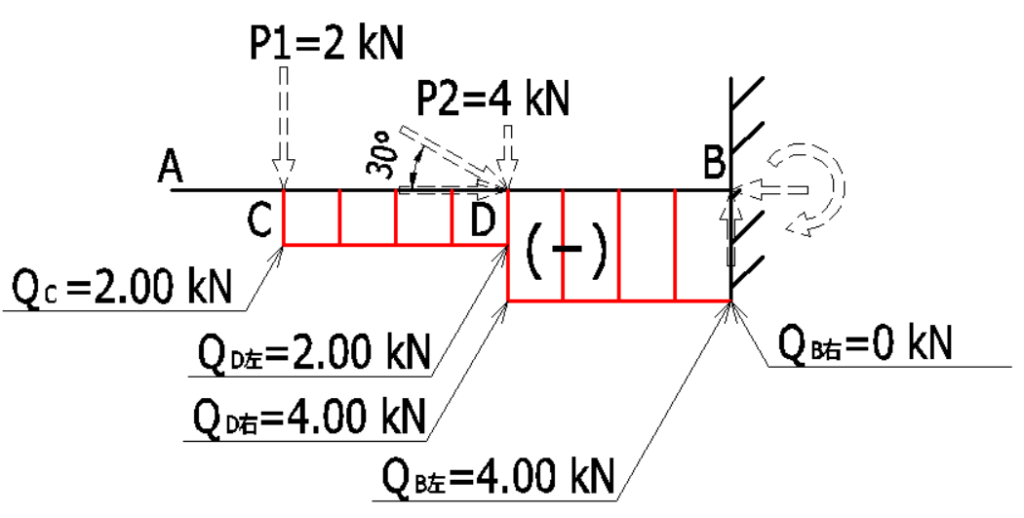
続いて、Q図を描きます。作用荷重を単純に落とし込んでいく作業です。
(1)A点のせん断力(=0)
(2)C点のせん断力
\(Q_A=P1=-2.00kN\)
(3)D点のせん断力
\(Q_C=P1+P2_y=-2.00-2.00=-4.00kN\)
以上より、片持ち梁のQ図は下記のようになります。
最後はN図を描きます。
単純梁のときと同様に、引張がプラス・圧縮がマイナスで表現します。
(1)A→C間
\(N=0\)
(2)C→D間
\(N=0\)
(3)D→B間
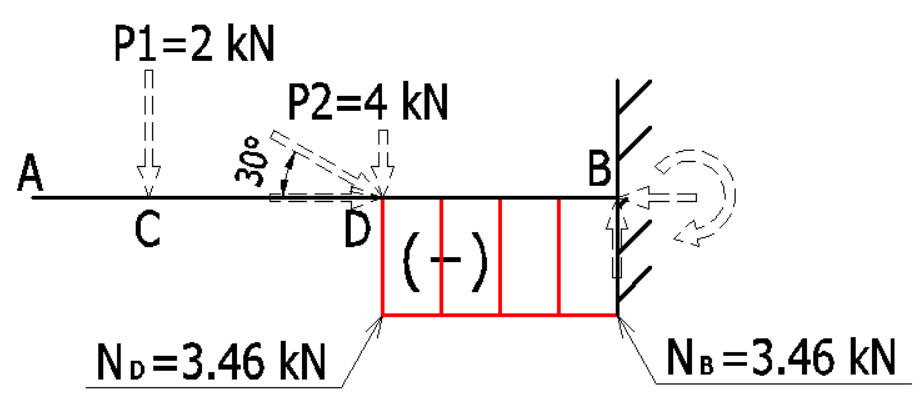
\(N_D=3.46kN\)(圧縮)
以上より、片持ち梁のN図は下記のようになります。