力のつりあいとは
一点・多点を問わず数個の力が物体に作用し、
物体が静止状態にあるとき
その物体は、つりあいの状態にあるといいます。
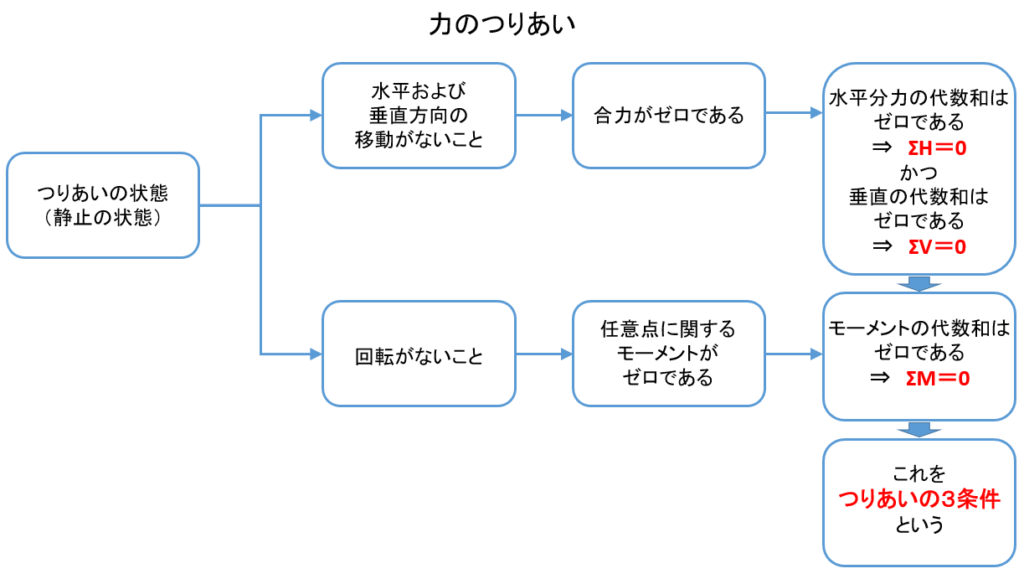
つりあいの3条件
\(\sum{H}=0\)・・・(1)
⇒水平方向の力の成分の代数和がゼロである
\(\sum{V}=0\)・・・(2)
⇒鉛直方向の力の成分の代数和がゼロである
\(\sum{M}=0\)・・・(3)
(1)(2)(3)が同時に成立します。
(3)は任意の点でモーメントがゼロになることを意味しています。
力の計算をする際、使用頻度の高い条件式です。
確実にマスターして、次のステップに進みましょう。
一点に作用する数個の力が作用する場合の力のつりあい条件
作用する力が一点に集中しているため回転はおこりません。
このため\( \sum(M)=0 \)は常に満足しています。
あとは、合力がゼロになる必要があります。
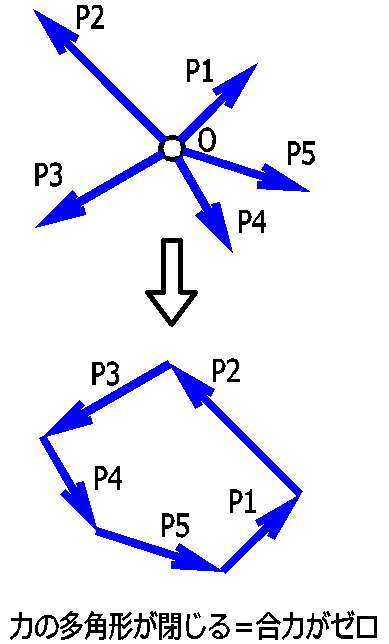
\(\overrightarrow{P_1}+\overrightarrow{P_2}+\overrightarrow{P_3}+\overrightarrow{P_4}+\overrightarrow{P_5}=0\)
計算で求める場合は、
\( \sum(H)=0 \) かつ \( \sum(V)=0 \)
を満足していることを確認します。ベクトルの成分で計算を行います。
\(\overrightarrow{P_1}=(a_1,b_1),\)
\(\overrightarrow{P_2}=(a_2,b_2),\)
\(\overrightarrow{P_3}=(a_3,b_3),\)
\(\overrightarrow{P_4}=(a_4,b_4),\)
\(\overrightarrow{P_5}=(a_5,b_5),\)とすると、
\(a_{1}+a_{2}+a_{3}+a_{4}+a_{5}=0\) かつ
\(b_{1}+b_{2}+b_{3}+b_{4}+b_{5}=0\) となります。
一点に作用しない数個の力が作用する場合の力のつりあい条件(塊のつりあい条件)
1点に作用しない数個の力がつりあうためには、合力がゼロになり、
かつ任意の点に関するモーメントがゼロである必要があります。
<実際に例題を解きながら確認してみましょう>
P1,P2,P3,P4がつりあっているとき、P2,P3,P4の大きさを求めよ。
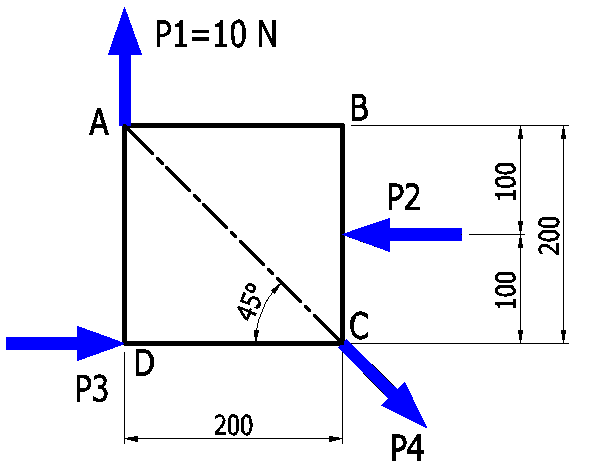
具体的にイメージするとしたら、
正方形の小さいテーブルをP1,P2,P3,P4で押したり引いたりしていますが、
動かない状態を思い浮かべてみてください。
力のつりあい条件を一つひとつ見ていきましょう。
\( \sum(H)=0 \)より
\(-P2+P3+P4\times\mathrm{cos}(45°)=0\) ・・・(1)式
\( \sum(V)=0 \)より
\(P1-P4\times\mathrm{sin}(45°)=0\) (\(\mathrm{sin}(45°)\)=\(\frac{1}{\sqrt{2}}\)より)
\(P4=P1\times\sqrt{2}\)
\(P4=10\sqrt{2}N\) ・・・(2)式
\( \sum{M_{D}}=0 \)より
\(P1\times200-P2\times100=0\)
\(10\times200=P2\times100\)
\(P2=20N\) ・・・(3)式
(2)式・(3)式を(1)に代入すると
\(-20+P3+10\sqrt{2}\times\frac{1}{\sqrt{2}}=0\)
\(P3=10N\)
となります。
このように、一点に作用しない力のつりあい条件は、
未知の力を導き出すときに使用します。

未知のベクトルを解き明かすときに使用する条件式です。
自分につりあう相手を探すより、
自分が見つけた好みの相手につりあうように
自分を高めていく生き方のほうがわたしは好きですね。
まとめ
力のつりあいとは、物体が静止し続けている状態のことです。
力学的には、
合力がゼロで、かつどこの点でもモーメントがゼロの状態です。
つりあいの状態で、方程式を3つ立てることができます。
- 水平方向の合力がゼロ
- 鉛直方向の合力がゼロ
- 任意の点でのモーメントがゼロ
上記の連立方程式を解くことで、静定梁の支点の反力を求めるときなど、
未知の力を導き出すことができます。
逆に言うと、つりあっている状態ならば、
上記の3つの条件が必ず成り立っているということです。
最も基本となる考え方のひとつです。
【関連記事】<静定梁とは>

