同一作用線上の力の特性
まず、力はベクトルで表現できるので、下記の特性を持っています。
(1)同一作用線上の力は移動ができます。
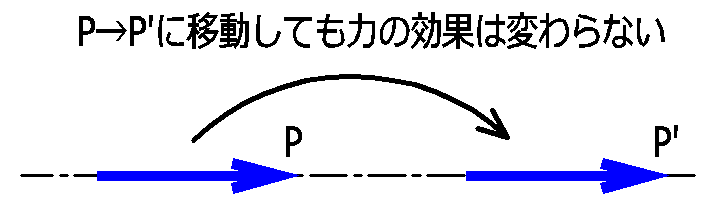
(2)同一作用線上の力は、簡単に足し算・引き算ができます。
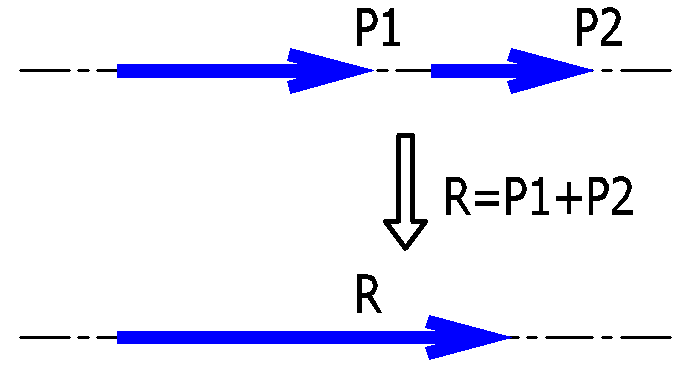
ベクトルの絶対値を足し算・引き算して求めることが可能ということです。
また、ベクトルの成分を計算式であらわすと、
\(\overrightarrow{P_1}=(a_1,b_1,c_1)\)
\(\overrightarrow{P_2}=(a_2,b_2,c_2)\)
と表現すると、
\(\overrightarrow{R}=\overrightarrow{P_1}+\overrightarrow{P_2}=(a_1+a_2,b_1+b_2,c_1+c_2)\)
一次元(直線)では(\(b_n=0,c_n=0\))⇒ベクトルの成分は\(a_n\)のみ
二次元(平面)では(\(c_n=0\))⇒ベクトルの成分は\(a_n,b_n\)
となります。これは、この次に説明する力の合力でも成立します。
【関連記事】<力とは>
力の合力
1つの物体に数個の力が作用するとき、これら数個の力をこれと全く同じ効果の1個の力に置き換えた場合、置き換えられた1個の力を合力といい、この合力を求めることを力の合成といいます。
ただし、ベクトルの絶対値ではなく、
ベクトルの成分で足し算する必要があります。
1点に作用する力の合力
おのおのの力(ベクトル)を順次継ぎ足していきます。
すべて継ぎ足した時、始点から終点に向けて引いた力(ベクトル)が合力です。
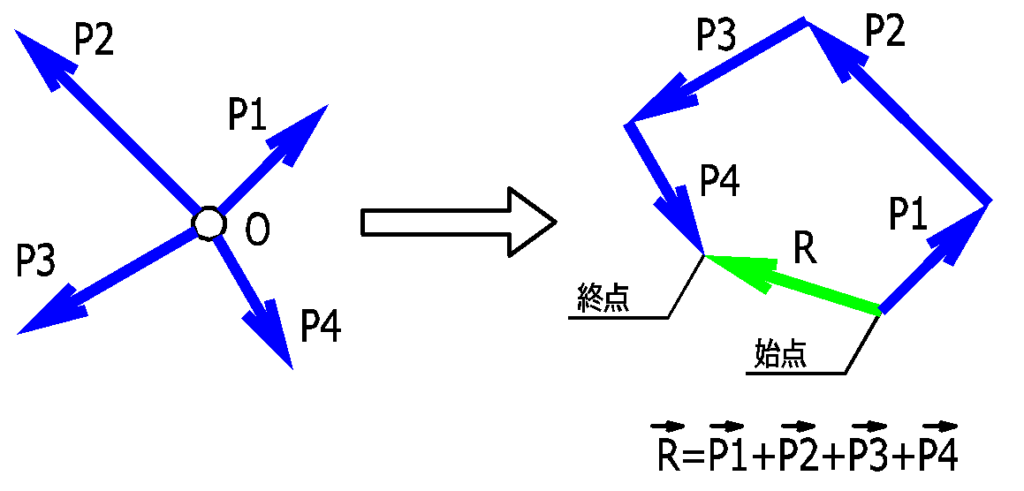
青色の矢印で表現された力(P1,P2,P3,P4)の合力は、緑色の矢印(R)の力になります。
これを力の多角形といいます。
ベクトルの継ぎ足す順番は、どんな順番でも結果は同じになります。
つまり、力の多角形のかたちが異なっても、最終的に求まる\(\overrightarrow{R}\)は同じになります。
1点で交わらない力の合成
1点に作用する力のときは、作用点を探す必要がありませんでしたが、
力の多角形で求めた合力が、どこに作用するのかをどうやって導き出すかがポイントになります。
1点で交わらない数個の力が作用するとき、
この合力は、連力図という図解法を用いて求めることができます。
連力図の描き方
(1)力の多角形を描き、合力の大きさと方向を求めます。
(2)任意の点にO(極)をとり、Oと各点を結び、極射線を描きます(1~4)
(3)この放射線(1~4)をもとの図の中に順に平行移動します。
※力の矢印と放射線の交点に次の放射線の端点を移動させるのがポイントです。
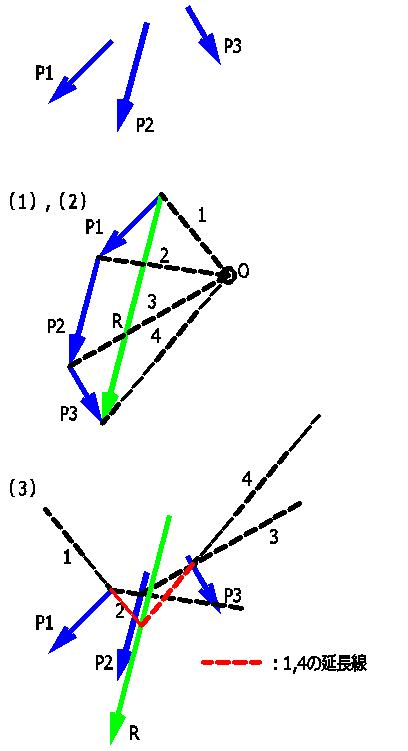
※もし補助線が、ベクトルと交わらなかった場合、
ベクトルを作用線上で移動させて交点を作りましょう。
補助線1,4の交点を合力Rが通ることになります。
連力図は、任意の点からの極射線を使って、
合力の作用線を導き出すことができます。
(連力図=示力図+極射線 の組合せ)
わたしは、構造力学の授業・試験でしか
連力図を使うことがありませんでした。
力の多角形をマスターできれば、まず問題ないと思います。
力の分解
1個の力を、これと同じ働きをする2個以上の力に分けることを、力の分解といいます。分解された力を、分力といいます。
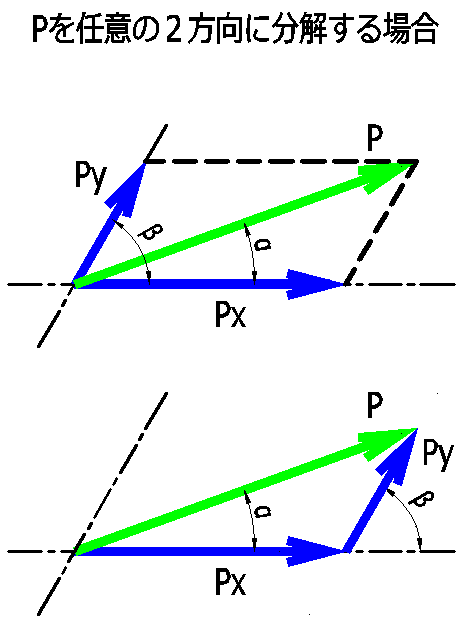
\(P_x=\Large{\frac{P\times\mathrm{sin}(β-α)}{\mathrm{sin}β}}\)
\(P_y=\Large{\frac{P\times\mathrm{sin}α}{\mathrm{sin}β}}\)
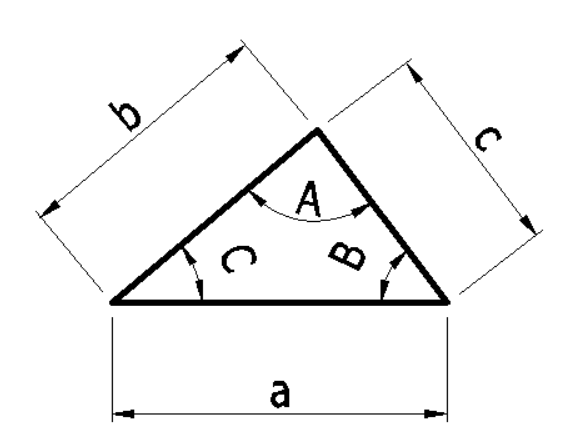
正弦定理より
\(\Large{\frac{a}{\sin{A}}}\)\(=\Large{\frac{b}{\sin{B}}}\)\(=\Large{\frac{c}{\sin{C}}}\)
を用いて求めています。
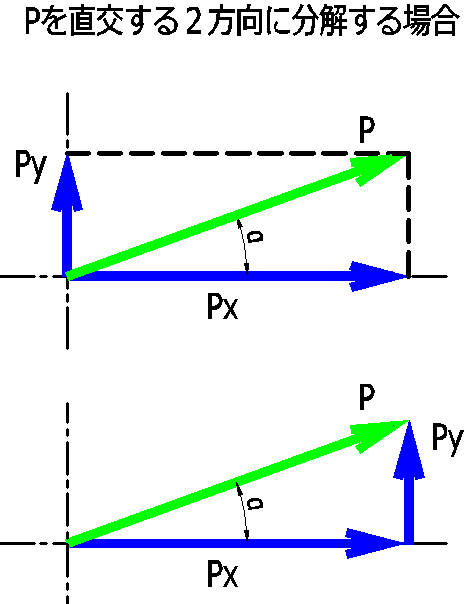
\(P_x=P\times\mathrm{cos}α\)
\(P_y=P\times\mathrm{sin}α\)
特に、直交する2方向に分解したとき、\(P_x\)を水平分力、\(P_y\)を垂直分力といいます。
まとめ
力の合成・分解は、ベクトルの足し算・引き算です。
力のつりあい条件式から、強度計算を行っていく際、ベースとなる考え方です。
しっかり理解して、ステップアップしていきましょう。
日頃から力の多角形を意識して力の流れを見る。
力をベクトルとして見える化するトレーニングをする、というのが大切です。
マラソンや筋トレなどと同じで、
一部のセンスのある方などは別ですが、
急に始めてすぐにうまくできるようになることは稀です。

