梁のせん断応力ってなに？

せん断応力とは

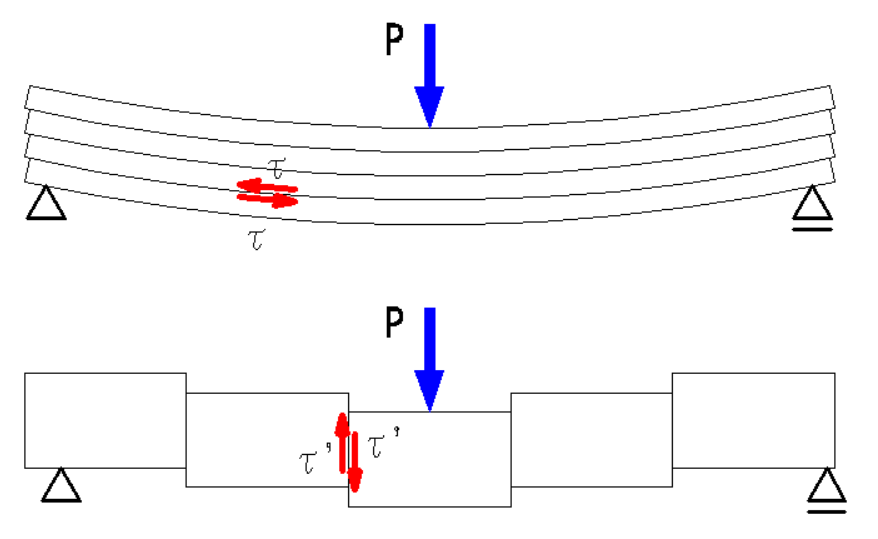
一般的に梁に曲げモーメントを受けると、同時にせん断力も受けます。

せん断力によって、梁の横断面・縦断面に生じる応力をせん断応力度といいます。

せん断応力度には、水平方向にずらす力に抵抗する水平せん断応力度（\(\tau\))と

鉛直方向にずらす力に抵抗する鉛直せん断応力度（\(\tau’\))があります。

水平せん断応力度と垂直せん断応力度の関係

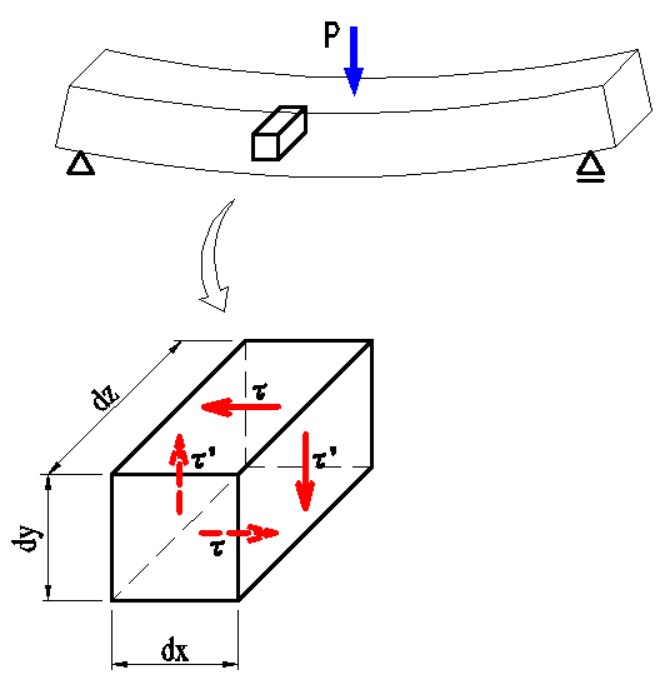
水平せん断応力度\(\tau\)と垂直せん断応力度\(\tau’\)は等しくなります。

水平せん断応力度と垂直せん断応力度が等しくなる理由

上図のように荷重を受けている梁（変形したまま静止状態）の

微小直方体を考えます。

この直方体の各面には、水平せん断力\(\tau\)と垂直せん断力\(\tau’\)生じ、

これらがつりあっています。ここで

　水平せん断力による偶力のモーメント\(=-(\tau\cdot{dx}\cdot{dz})dy\)

　垂直せん断力による偶力のモーメント\(=(\tau’\cdot{dy}\cdot{dz})dx\)

つりあいの条件より、このふたつの偶力のモーメントの合力はゼロになるので

　\(\sum{M}=0\)より

　\(-(\tau\cdot{dx}\cdot{dz})dy+(\tau’\cdot{dy}\cdot{dz})dx=0\)

　\(\tau=\tau’\)

以上より、水平せん断応力度と垂直せん断応力度は等しいということです。

せん断応力度の一般式

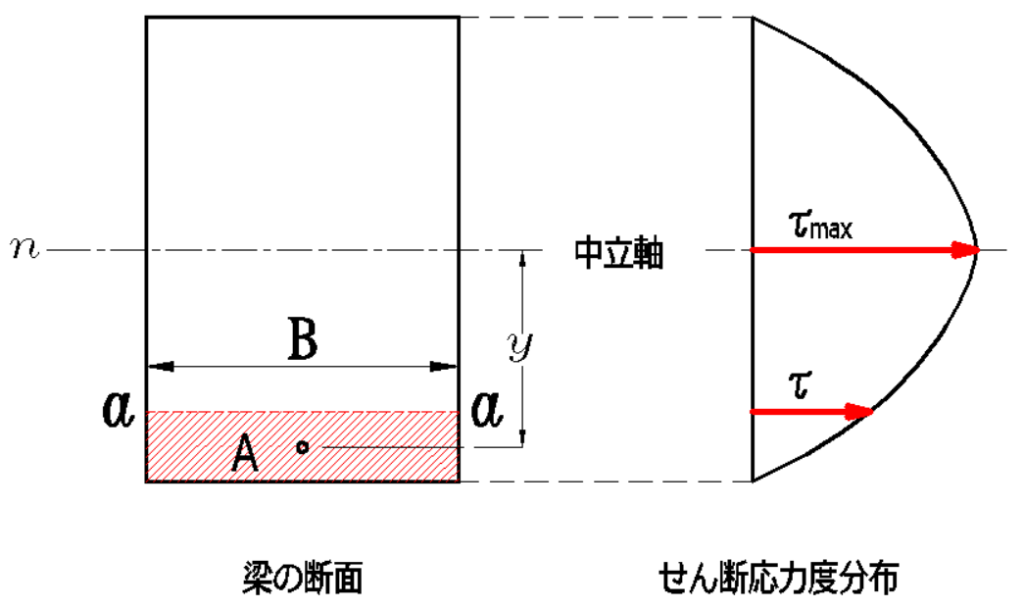
\(Q\)：外力によって生じるせん断力

\(S_n\)：a-a面より外側の断面（赤斜線部）の中立軸に関する断面一次モーメント（\(=A\cdot{y}\)）

\(B\)：a-a面の幅

\(I_n\)：中立軸に関する断面二次モーメント

とすると、せん断応力度の一般式は、

　\(\tau=\Large{\frac{Q\cdot{S_n}}{B\cdot{I_n}}}\)（\(N/mm^2\)）

となります。

せん断応力度の一般式の導き出し方

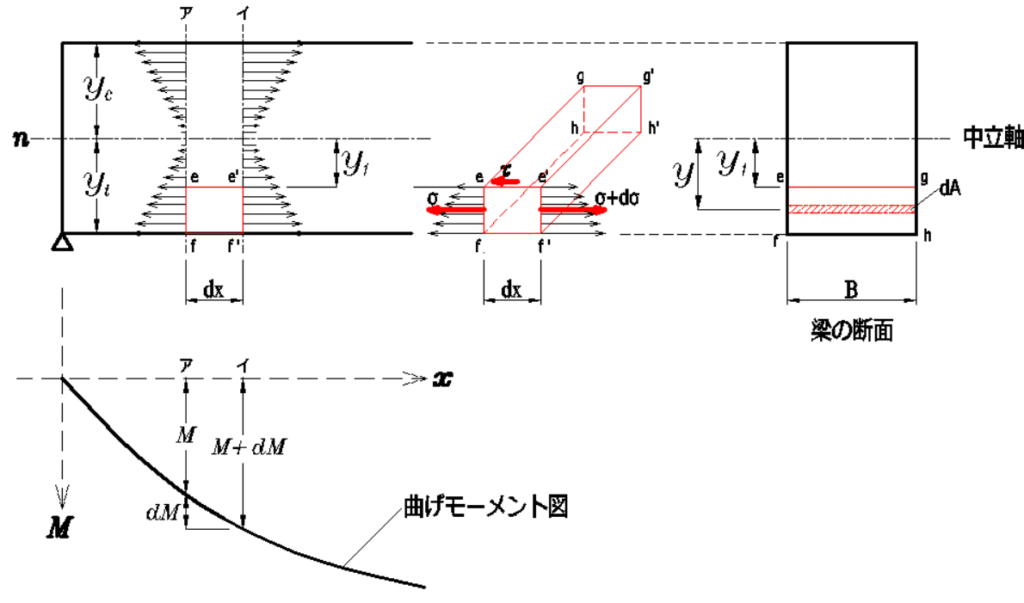
梁の任意の断面ア－アに作用する曲げモーメントをM

断面ア－アから微小距離dxの断面イ－イに作用する曲げモーメントをM＋dMとします。

いま、\(y=y_1\)から\(y=y_t\)の間の、微小六面体（efgh-e’f’g’h’）について考えます。

（1）中立軸からyの位置のア－ア断面の曲げ応力度

　\(\sigma=\Large{\frac{M\cdot{y}}{I_n}}\)

（2）中立軸からyの位置のイ－イ断面の曲げ応力度

　\(\sigma+d\sigma=\Large{\frac{(M+dM)\cdot{y}}{I_n}}\)

（3）微小六面体の左側（efgh）の曲げ応力度

　\(\Large{\int^{y_t}_{y_1}}\)\(\sigma\cdot{dA}=\Large{\int^{y_t}_{y_1}\frac{M\cdot{y}}{I_n}}\)\(\cdot{dA}\)

（4）微小六面体の左側（e’f’g’h’）の曲げ応力度

　\(\Large{\int^{y_t}_{y_1}}\)\(（\sigma+d\sigma）\cdot{dA}=\Large{\int^{y_t}_{y_1}\frac{（M+dM）\cdot{y}}{I_n}}\)\(\cdot{dA}\)

このことから、e’f’g’h’の曲げ応力度は、efghの曲げ応力度より大きいので、

微小六面体がつりあいを保つためには、ee’gg’面にせん断応力度\(\tau\)が生じていなければならない。

このせん断応力度を足し合わせた合計は、

　\(\tau\cdot{B}\cdot{dx}\)

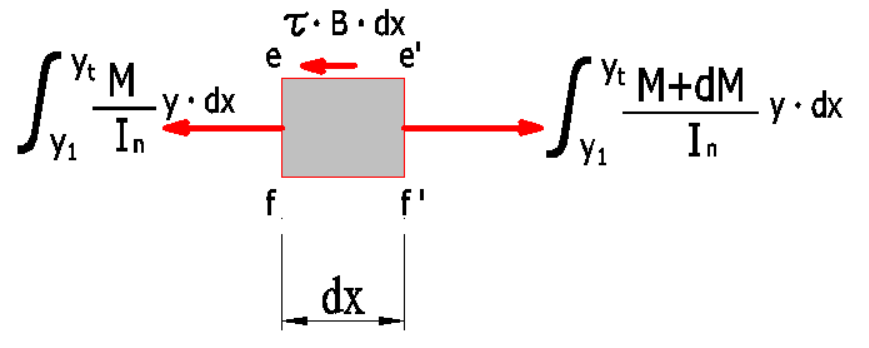
　\(\tau\cdot{B}\cdot{dx}=\Large{\int^{y_t}_{y_1}\frac{（M+dM）\cdot{y}}{I_n}}\)\(\cdot{dA}-\Large{\int^{y_t}_{y_1}\frac{M\cdot{y}}{I_n}}\)\(\cdot{dA}\)

　　　　　　　\(=\Large{\int^{y_t}_{y_1}\frac{dM\cdot{y}}{I_n}}\)\(\cdot{dA}\)

　\(\tau=\Large{\frac{1}{B\cdot{I_n}}\int^{y_t}_{y_1}\frac{dM\cdot{y}}{dx}}\)\(\cdot{dA}\)

ここで、

　\(\Large{\frac{dM}{dx}}\)\(=Q\)

また、e-e’より外側の断面の中立軸に関する断面一次モーメントは、

　\(S_n=\Large{\int^{y_t}_{y_1}}\)\(y\cdot{dA}\)

とあらわされるので、

　\(\tau=\Large{\frac{Q\cdot{S_n}}{B\cdot{I_n}}}\)（\(N/mm^2\)）

となります。

長方形断面のせん断応力度

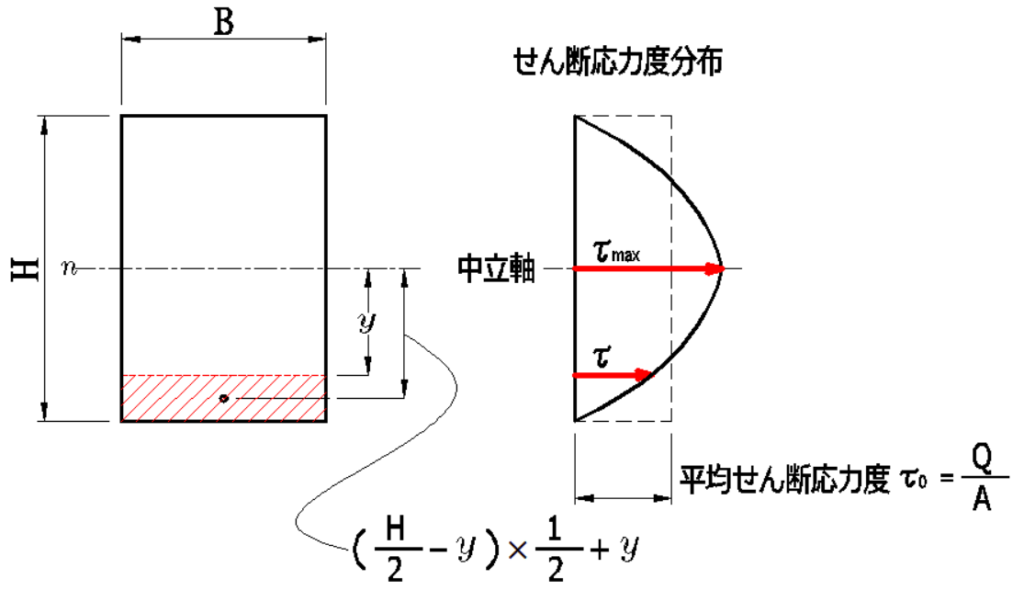
平均せん断応力度は

　\(\tau_0=\Large{\frac{Q}{A}}\)

中立軸から斜線部面積図心までの距離の式を変形します。

　\((\Large{\frac{H}{2}}\)\(-y)\times\Large{\frac{1}{2}}\)\(+y\)\(=\Large{\frac{1}{2}}\)\((\Large{\frac{H}{2}}\)\(+y)\)

中立軸に関する斜線部面積の断面一次モーメント

　\(S_x=B\cdot{(}\Large{\frac{H}{2}}\)\(-y)\times{\Large{\frac{1}{2}}}\)\((\Large{\frac{H}{2}}\)\(+y)\)\(=\Large{\frac{B}{2}}\)\((\Large{\frac{H^2}{4}}\)\(-y^2)\)

中立軸に関する断面二次モーメントは

　\(I_n=\Large{\frac{BH^3}{12}}\)

より、

　\(\tau=\Large{\frac{Q}{B}}\)\(\cdot\Large{\frac{12}{BH^3}}\)\(\cdot\Large{\frac{B}{2}}\)\((\Large{\frac{H^2}{4}}\)\(-y^2)\)\(=\Large{\frac{6Q}{BH^3}}\)\((\Large{\frac{H^2}{4}}\)\(-y^2)\)

（1）\(y=\Large{\frac{H}{2}}\)　のとき、\(\tau=0\)　となります。

⇒断面の上縁、下縁のせん断応力度はゼロということです。

（2）\(y=0\)　のとき、\(\tau_{max}=\Large{\frac{3}{2}}\)\(\cdot\Large{\frac{Q}{BH}}\)　となります。

平均せん断応力度を\(\tau_0\)とすると、

　\(\tau_{max}=\Large{\frac{3}{2}}\)\(\tau_0\)

となります。

円形断面のせん断応力度

同様に、円形断面のせん断応力度を求めてみましょう。

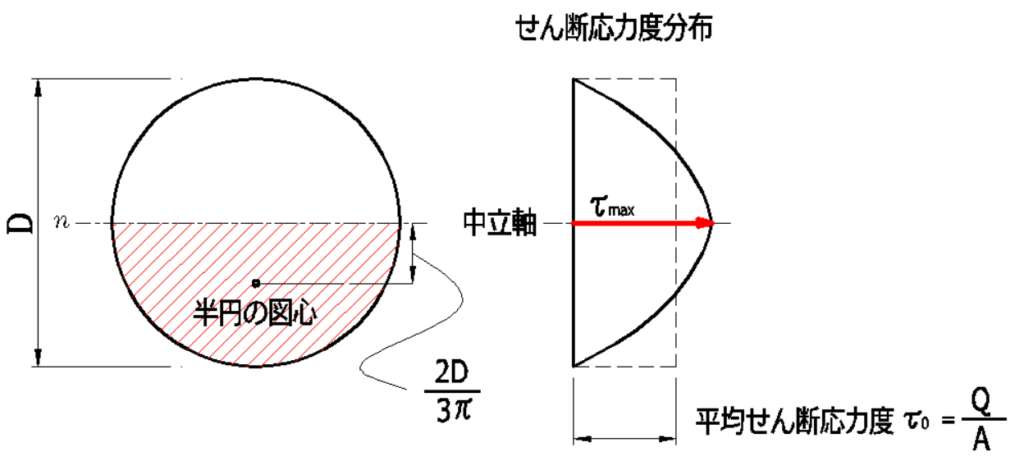
円の断面積は、

　\(A=\Large{\frac{\pi{D^2}}{4}}\)

斜線部面積の中立軸の断面一次モーメントは、

　\(S_n=\Large{\frac{\pi{D^2}}{4}}\)\(\times\Large{\frac{1}{2}}\)\(\times\Large{\frac{2D}{3\pi}}\)

中立軸に関する断面二次モーメントは、

　\(I_n=\Large{\frac{\pi{D^4}}{64}}\)

と表せられます。

平均せん断応力度は、

　\(\tau_0=\Large{\frac{Q}{A}}\)\(=\Large{\frac{Q}{\frac{\pi{D^2}}{4}}}\)

中立軸で最大せん断応力度が生じるので、

　\(\tau_{max}=\Large{\frac{Q\cdot{S_n}}{D\cdot{I_n}}}\)\(=Q\times\Large{\frac{\pi{D^2}}{4}}\)\(\times\Large{\frac{1}{2}}\)\(\times\Large{\frac{2D}{3\pi}}\)\(\times\Large{\frac{1}{D}}\)\(\times\Large{\frac{64}{\pi{D^4}}}\)\(=\Large{\frac{4}{3}}\)\(\cdot\Large{\frac{Q}{\frac{\pi{D^2}}{4}}}\)\(=\Large{\frac{4}{3}}\)\(\cdot\tau_0\)