付着とは
鉄筋コンクリート構造は、鉄筋とコンクリート一体となって
荷重に抵抗することが前提となっています。
コンクリートから鉄筋へ、また鉄筋からコンクリートへ、
スムーズに荷重を伝達し、一体化するために、
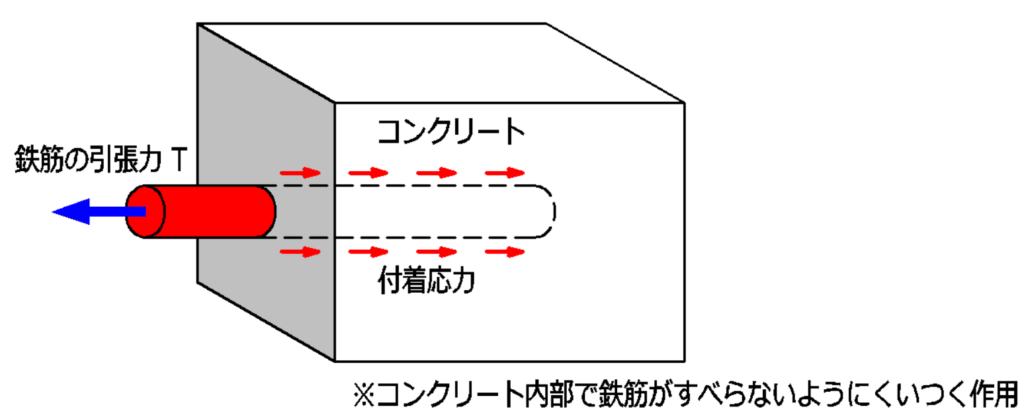
鉄筋がコンクリートの境界面にくいついて
ズレ止めのように働く作用のことを付着といいます。
許容付着応力度
Fc:コンクリートの設計基準強度 とすると
許容付着応力度は下記のようになります。
鉄筋のコンクリートに対する許容付着応力度(\(N/mm^2\))
| 材料 | 長期 上端筋 | 長期 その他の鉄筋 | 短期 上端筋・その他の鉄筋 |
|---|---|---|---|
| 異形鉄筋 | \(\Large{\frac{1}{15}}\)\(F_c\)かつ (\(0.9+\Large{\frac{2}{75}}\)\(F_c\))以下 | \(\Large{\frac{1}{10}}\)\(F_c\)かつ (\(1.35+\Large{\frac{1}{25}}\)\(F_c\))以下 | 長期に対する値の1.5倍 |
| 丸鋼 | \(\Large{\frac{4}{100}}\)\(F_c\)かつ、\(0.9\)以下 | \(\Large{\frac{6}{100}}\)\(F_c\)かつ、\(1.35\)以下 | 長期に対する値の1.5倍 |
上端筋とは、曲げ材にあってその鉄筋の下に300mm以上のコンクリートが打ち込まれる場合の水平鉄筋をいいます。
異形鉄筋で、鉄筋までのコンクリートかぶり厚が鉄筋の径の1.5倍未満の場合には、付着応力度は、この表の値に「かぶり厚さ/鉄筋径の1.5倍」を乗じた値とします。
上端筋の付着応力度を低減する理由
コンクリートのブリージングや、骨材の沈み込みにより鉄筋下部に空隙ができます。
その結果、付着力が小さくなるのでその他の鉄筋の2/3倍になっています。

付着割裂破壊
付着割裂破壊は、主筋に沿って生じるひび割れです。
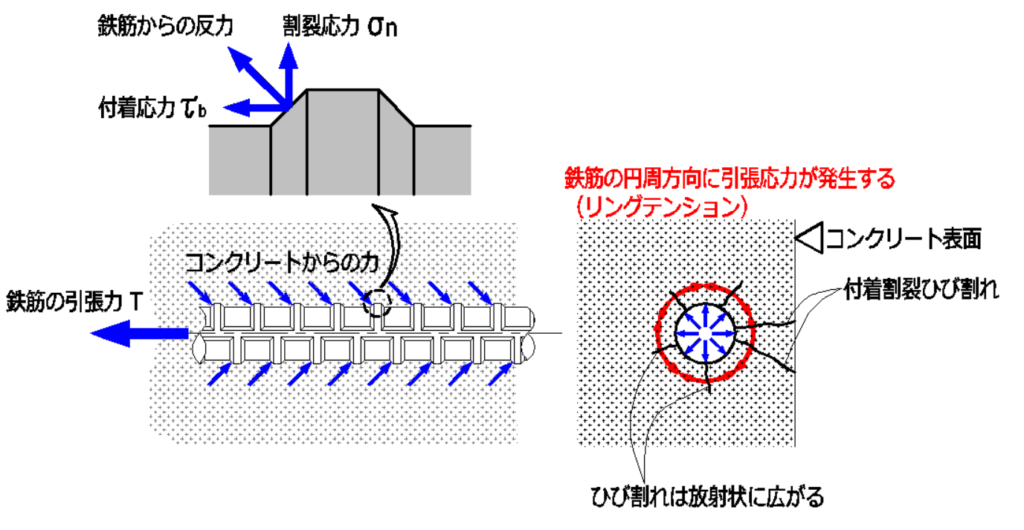
下図のように、異形鉄筋に引張力が作用すると、
コンクリートはその引張力に抵抗しようと部材内部で鉄筋を抑えようとします。
これは、鉄筋がコンクリートを押し広げようとする力(\(\sigma_n\))が働き、
その結果として、コンクリートには鉄筋の円周方向に引張応力(リングテンション)が発生します。
この引張応力(リングテンション)が引張耐力を超えてしまうとひび割れが生じます。
ひび割れは放射状に広がり、かぶり厚が小さい部分などでは表面にまで達し、
コンクリートと鉄筋の一体性が失われてしまいます。
付着割裂の基準となる強度fb
| 材料 | 上端筋 | その他の鉄筋 |
|---|---|---|
| 普通コンクリート | \(0.8\times(\Large{\frac{F_c}{40}}\)\(+0.9)\) | \(\Large{\frac{F_c}{40}}\)\(+0.9\) |
| 軽量コンクリート | 普通コンクリートの値の0.8倍 | 普通コンクリートの値の0.8倍 |
丸鋼は、ふしがないため生じません。
異形鉄筋の付着割裂パターン
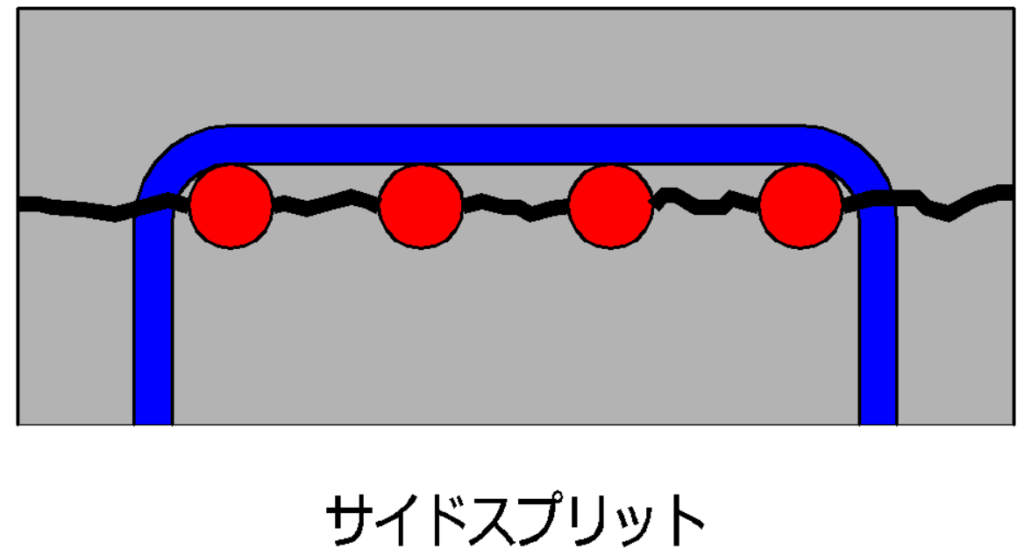
サイドスプリット
ひび割れが鉄筋を端から端まで貫通している状態。
コーナースプリット
ひび割れがコーナー部の鉄筋を貫通している状態。

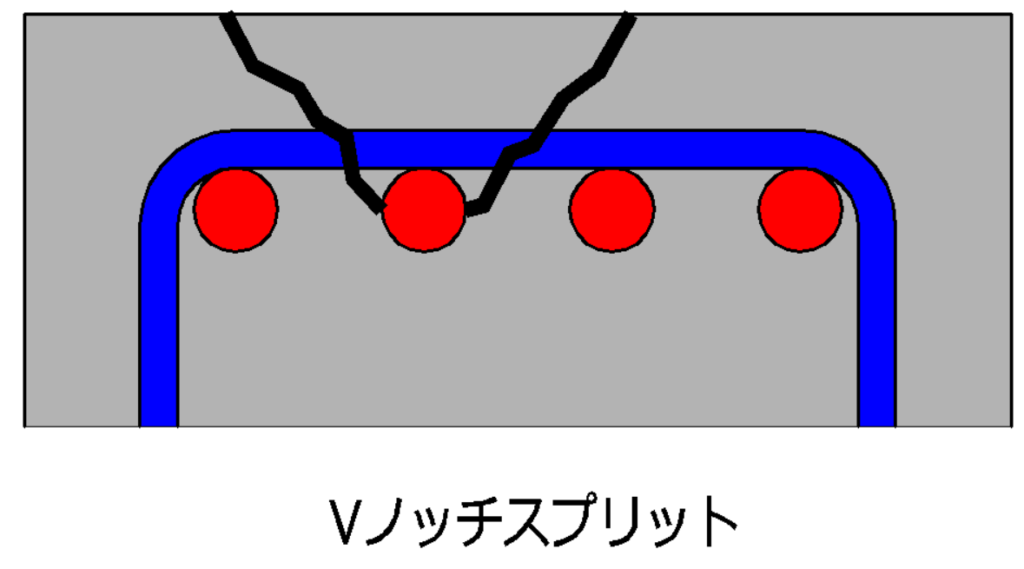
Vノッチスプリット
ひび割れが真ん中の鉄筋をえぐるように走っている状態。
定着と付着
付着を確保するため、鉄筋を構造体に十分飲み込ませることを定着といいます。
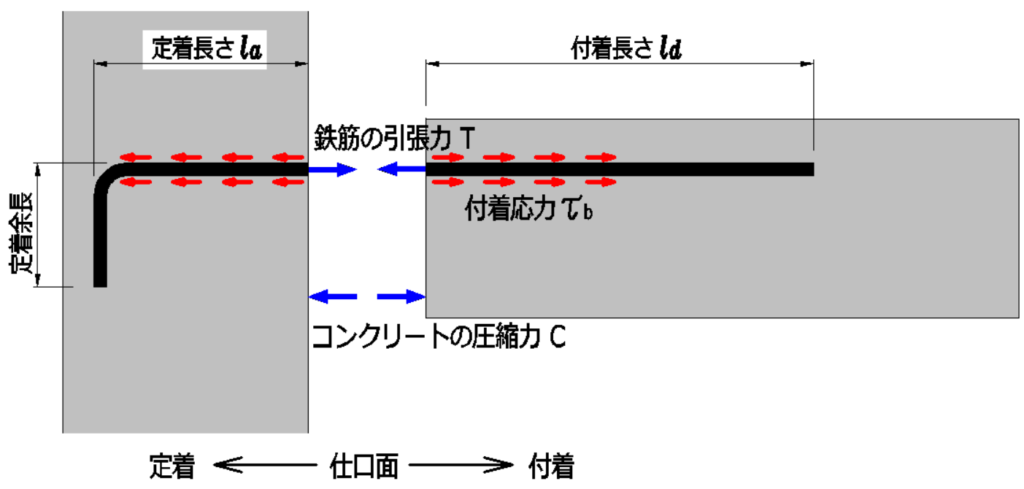
上図では、梁の主筋の付着:定着先は柱の仕口部 ということです。
因果関係に順番があります。
付着の検定
曲げ材の引張鉄筋は、下記の付着応力度の検定を行います。
使用限界
長期荷重時の曲げ補強鉄筋の付着性に関して、使用性が確保されることを確認
損傷限界
短期荷重時の曲げ補強鉄筋の付着性に関して、損傷制御できることを確認
安全限界
大地震時に曲げ補強鉄筋に沿って付着割裂破壊が生じないことにより
安全性が確保されることを確認
付着検定断面
付着検定を行う断面は
- スパン内で最大曲げモーメントとなる断面(通常部材端部)
- スパン内で減じられる鉄筋が計算上不要となる断面
カットオフ筋とは
スパンの途中で切断され、減じられる鉄筋をカットオフ筋といいます。
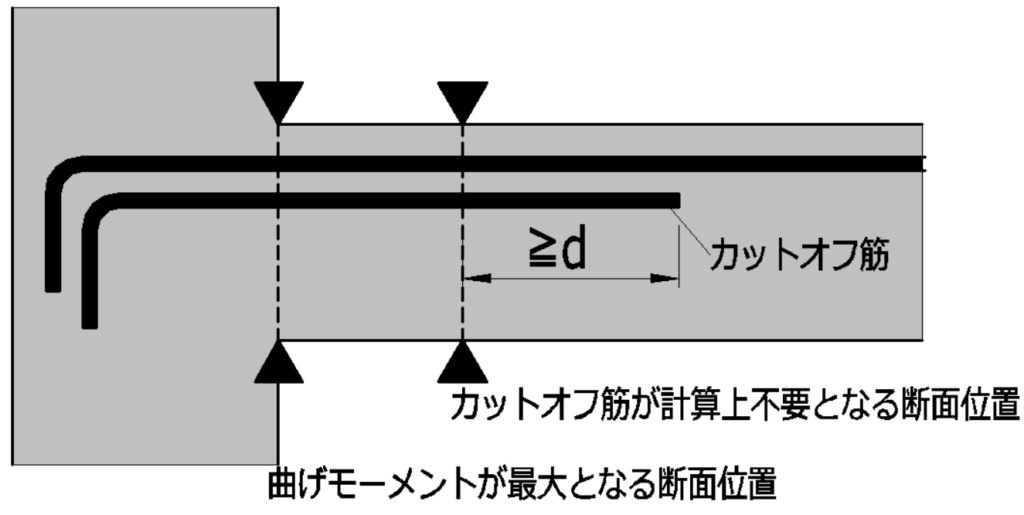
付着長さldの採り方
付着長さの採り方は、スパン内に通しで配筋されるものと、カットオフ筋で異なります。
スパン内に通しで配筋される鉄筋の付着長さ
(1)スパンの両端が、曲げ降伏する場合(=両端に塑性ヒンジが生じる場合)
L:曲げ材の内法長さ
d:曲げ材の有効せい
1.1)塑性ヒンジ部にひび割れが生じるとき
\(l_d=\Large{\frac{L+d}{2}}\)
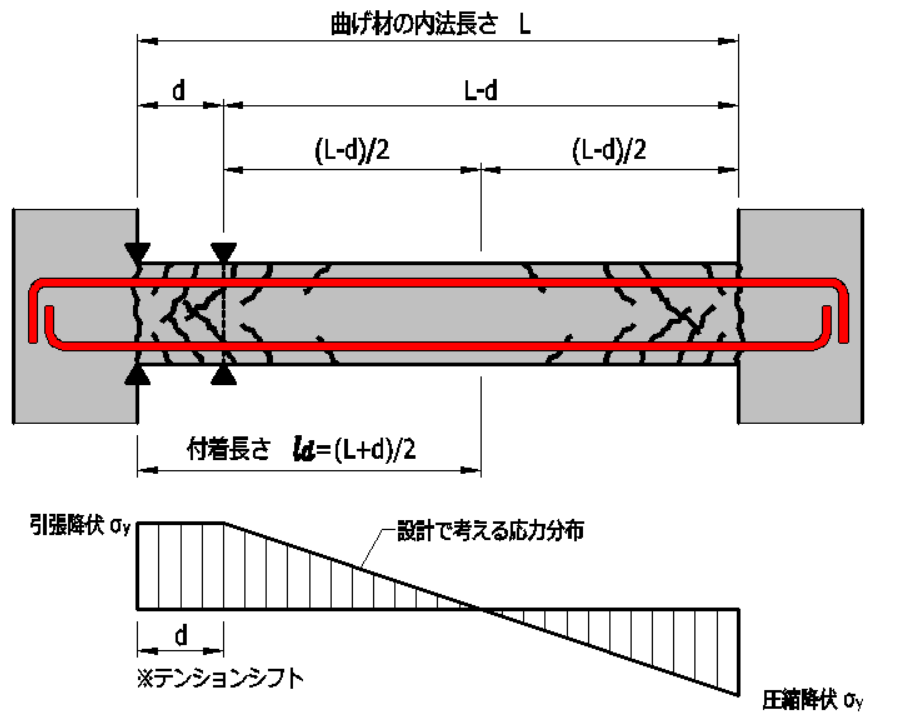
\(\Large{\frac{(L+d)}{2}}\)となります。
1.2)塑性ヒンジ部にひび割れが生じないと確認できたとき
\(l_d=\Large{\frac{L}{2}}\)
(2)スパンの一端のみが降伏し他端は弾性応力の場合、または両端が弾性応力の場合
\(l_d=L\)
スパンの途中でカットオフされる鉄筋の付着長さ
付着検定断面から鉄筋端までの長さ。
鉄筋端部に標準フックを設ける場合は、付着検定断面から
フック開始点までの長さを付着長さとします。

端部にフックを設けた場合、
引張鉄筋に作用する存在応力度\(\sigma_t\)を2/3倍に小さくすることが認められています。
これは、フック部で残りの1/3を負担すると仮定することは、
経験的に安全側に評価できるとみなされているためです。
コーン状破壊の検定を行うことが、より実際に即した評価になります。
ということなんですね。
仕口内への定着を検定するときには
適用されていません。
テンションシフトとは
付着検定断面の鉄筋の引張応力度\(\sigma_t\)がA検定断面よりおよそd(断面の有効せい)
だけ離れた断面まで一定に分布するとみなし、B断面より一様な付着作用によって
定着されるものと仮定することを、テンションシフトといいます。
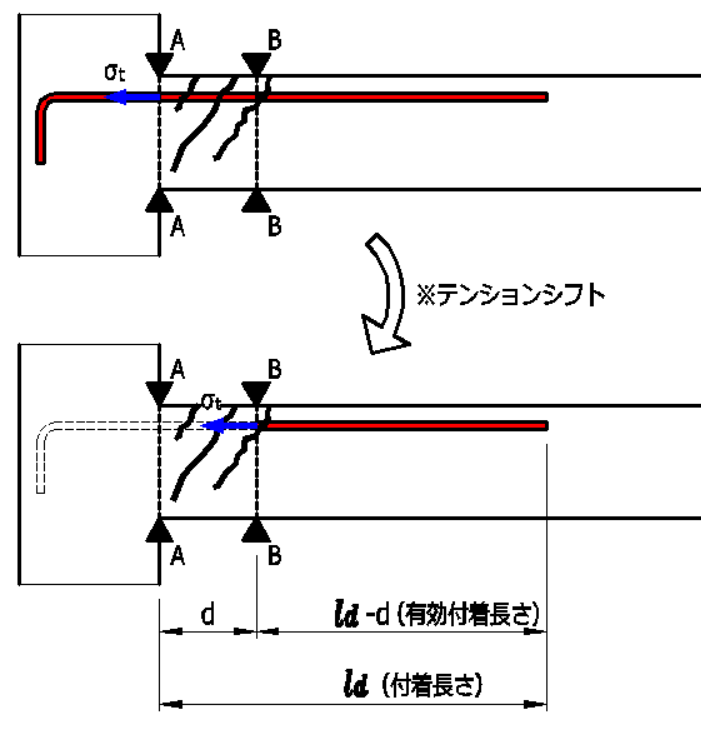
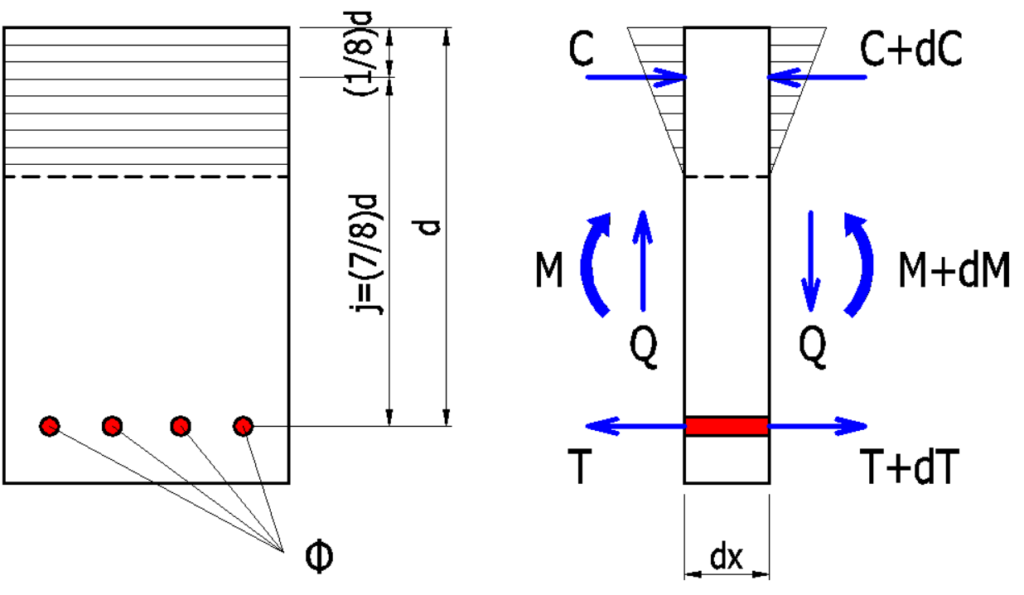
曲げ材の引張鉄筋の付着応力度の検定式
\(dT=\Large{\frac{dM}{j}}\)
\(dT=\tau_{a1}\cdot\phi\cdot{dx}\)、
\(\Large{\frac{dM}{j}}\)\(=\tau_{a1}\cdot\phi\cdot{dx}\)
\(\tau_{a1}=\Large{\frac{dM}{dx\cdot\phi\cdot{j}}}\)また、\(\Large{\frac{dM}{dx}}\)\(=Q\)より
\(\tau_{a1}=\Large{\frac{Q}{\sum\cdot\phi\cdot{j}}}\)(\(N/mm^2\))(曲げ付着応力度)
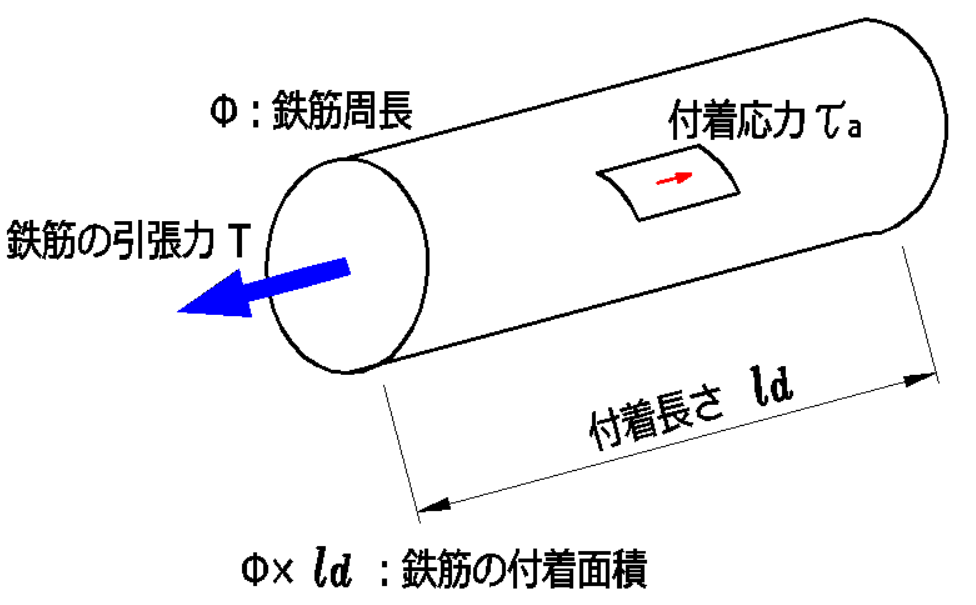
\(\tau_{a2}=\Large{\frac{\sigma_t\cdot{a}}{\phi\cdot(l_d-d)}}\)
\(a=\Large{\frac{d_b^2\cdot\pi}{4}}\)(:鉄筋の断面積)
\(\phi=d_b\cdot\pi\)(:鉄筋の周長)
\(\tau_{a2}=\Large{\frac{\sigma_t\cdot{d_b}}{4\cdot(l_d-d)}}\)(\(N/mm^2\))(平均付着応力度)
(=分母が大きくなる)
厳しく検定するため、
鉄筋の付着応力度\(f_a\)の0.8倍の数値で検定を行います。
\(\tau_{a1}\):引張鉄筋の曲げ付着応力度(\(N/mm^2\))
\(\tau_{a2}\):引張鉄筋の平均付着応力度(\(N/mm^2\))
\(\tau_{y}\):引張鉄筋の降伏時の平均付着応力度(\(N/mm^2\))
\(Q_L\):長期荷重時せん断力(\(N\))
\(Q_E\):水平荷重時せん断力(\(N\))
\(\phi\):引張鉄筋の周長(\(mm\))
\(j\):曲げ材の応力中心距離(\(mm\))。\(j=\Large{\frac{7}{8}}\)\(d\)とすることができます。
\(d\):曲げ材の有効せい(\(mm\))
\(l_d\):引張鉄筋の付着長さ(\(mm\))
\(_{L}\sigma_t\):付着検定断面位置における長期荷重時の鉄筋の存在応力度(\(N/mm^2\))
\(_{S}\sigma_t\):付着検定断面位置における短期荷重時の鉄筋の存在応力度(\(N/mm^2\))
\(\sigma_y\):付着検定断面位置における鉄筋の降伏強度(\(N/mm^2\))
\(_{L}f_a\):コンクリートに対する鉄筋の長期付着応力度(\(N/mm^2\))
\(_{S}f_a\):コンクリートに対する鉄筋の短期付着応力度(\(N/mm^2\))
\(f_b\):付着割裂の基準となる強度(\(N/mm^2\))
\(d_b\):検討対象鉄筋径。異形鉄筋の場合は呼び名の数値(\(mm\))(D25⇒25mm)
検定の条件で荷重がかかった時、生じている反力です。
「因果」でいうと、「果の方」の応力です。
長期荷重に対する使用性確保の確認
\(\tau_{a1}=\Large{\frac{Q_L}{\sum{\phi\cdot{j}}}}\)\(\leq{_Lf_a}\)(\(N/mm^2\))
または、
\(\tau_{a2}=\Large{\frac{_L\sigma_t\cdot{d_b}}{4(l_d-d)}}\)\(\leq{0.8_Lf_a}\)(\(N/mm^2\))
を確認します。
短期荷重に対する損傷制御の確認
\(\tau_{a1}=\Large{\frac{Q_L+Q_E}{\sum{\phi\cdot{j}}}}\)\(\leq{_Sf_a}\)(\(N/mm^2\))
または、
\(\tau_{a2}=\Large{\frac{_S\sigma_t\cdot{d_b}}{4(l_d-d)}}\)\(\leq{0.8_Sf_a}\)(\(N/mm^2\))
を確認します。
大地震時に対する安全性の確保
\(\tau_{y}=\Large{\frac{\sigma_y\cdot{d_b}}{4(l_d-d)}}\)\(\leq{K\cdot{f_a}}\)(\(N/mm^2\))
を確認します。ここで、
\(K\):配筋の状態による割増係数
\(C\):鉄筋間のあき、または最小かぶり厚さの3倍の値のうちの小さい方の数値で、\(5d_s\)以下(\(mm\))
\(W\):付着割裂面を横切る横補強筋効果を表す換算長さ。\(2.5d_s\)以下(\(mm\))
\(A_{st}\):付着割裂面を横切る横補強筋の断面積の合計(\(mm^2\))
\(s\):横補強筋のピッチ(\(mm\))
\(N\):引張鉄筋の本数
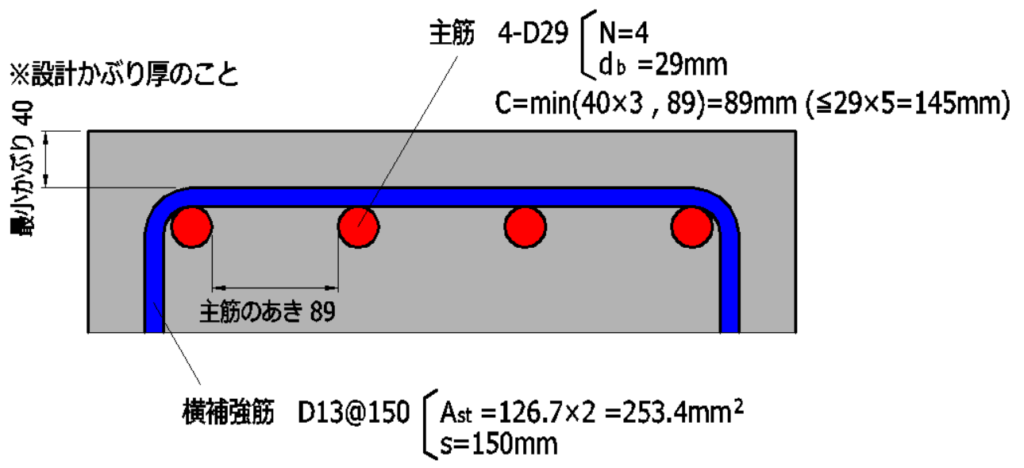
\(K=0.3(\Large{\frac{C+W}{d_s}}\)\()+0.4\leq2.5\)
\(W=80\Large{\frac{A_{st}}{s\cdot{N}}}\)\(\leq2.5d_s\)(\(mm\))
まとめ
付着とは、コンクリートに対する鉄筋の一体性のことです。
長期荷重時・短期荷重時・大地震時、それぞれの荷重が作用したときに
この一体性を確保できるか検定を行います。
参考文献
- 日本建築学会(2010年)「鉄筋コンクリート構造計算規準・同解説」
- 佐藤立美・荒木秀夫・森村毅(2011年)「RC規準による鉄筋コンクリートの構造設計[改訂版]」鹿島出版会

